
分析 (I)利用倍角公式与两角和差的正弦公式可得:f(x)=$\frac{1}{2}$sin(2x+A)-$\frac{1}{2}$sinA,根据f(x)的最大值为$\frac{1}{4}$,可得$\frac{1}{2}-\frac{1}{2}sinA$=$\frac{1}{4}$,解得$A=\frac{π}{6}$,可得f(x)=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)-$\frac{1}{4}$,再利用正弦函数的单调性即可得出.
(II)由余弦定理可得:a2=b2+c2-2bccosA解得c.利用S△ABC=$\frac{1}{2}bcsinA$即可得出.
解答 解:(I)f(x)=$\frac{1}{2}$sin2xcosA-sinA$•\frac{1-cos2x}{2}$=$\frac{1}{2}$(sin2xcosA+sinAcos2x)-$\frac{1}{2}$sinA=$\frac{1}{2}$sin(2x+A)-$\frac{1}{2}$sinA,
∵f(x)的最大值为$\frac{1}{4}$,
∴$\frac{1}{2}-\frac{1}{2}sinA$=$\frac{1}{4}$,化为sinA=$\frac{1}{2}$,
∵△ABC是锐角三角形,∴$A=\frac{π}{6}$,
∴f(x)=$\frac{1}{2}$sin(2x+$\frac{π}{6}$)-$\frac{1}{4}$,由$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}$$≤\frac{π}{2}+2kπ$,(k∈Z),
解得$kπ-\frac{π}{3}$≤x≤k$π+\frac{π}{6}$(k∈Z).
∴函数f(x)的单调递增区间为$[kπ-\frac{π}{3},kπ+\frac{π}{6}]$(k∈Z).
(II)由余弦定理可得:a2=b2+c2-2bccosA,
∴$13={7}^{2}+{c}^{2}-14c×cos\frac{π}{6}$,化为${c}^{2}-7\sqrt{3}c+36$=0,解得c=$3\sqrt{3}$或4$\sqrt{3}$.
经过检验可得:$c=3\sqrt{3}$不符合题意,舍去.∴c=4$\sqrt{3}$.
∴S△ABC=$\frac{1}{2}bcsinA$=$\frac{1}{2}×7×4\sqrt{3}×\frac{1}{2}$=7$\sqrt{3}$.
点评 本题考查了倍角公式、两角和差的正弦公式、正弦函数的单调性、余弦定理、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | K的最大值为$\frac{1}{e}$ | B. | K的最小值为$\frac{1}{e}$ | C. | K的最大值为2 | D. | K的最小值为2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 “十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.
“十一黄金周”期间某市再次迎来了客流高峰,小李从该市的A地到B地有L1、L2两条路线(如图),L1路线上有A1、A2、A3三个路口,各路口遇到堵塞的概率均为$\frac{2}{3}$;L2路线上有B1、B2两个路口,各路口遇到堵塞的概率依次为$\frac{3}{4}$、$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
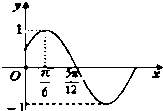 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,令${a_n}=f(\frac{nπ}{6})$,则a1+a2+a3+…+a2014=0.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,令${a_n}=f(\frac{nπ}{6})$,则a1+a2+a3+…+a2014=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com