
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() 的右准线方程为
的右准线方程为![]() ,右顶点为
,右顶点为![]() .
.

![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 若M,N是椭圆C上不同于A的两点,点P是线段MN的中点.
若M,N是椭圆C上不同于A的两点,点P是线段MN的中点.
![]() 如图1,若
如图1,若![]() 为等腰直角三角形且直角顶点P在x轴上方,求直线MN的方程;
为等腰直角三角形且直角顶点P在x轴上方,求直线MN的方程;
![]() 如图2所示,点Q是线段NA的中点,若
如图2所示,点Q是线段NA的中点,若![]() 且
且![]() 的角平分线与x轴垂直,求直线AM的斜率.
的角平分线与x轴垂直,求直线AM的斜率.
【答案】(1)![]() ; (2)①
; (2)①![]() ;②
;②![]() .
.
【解析】
(1)利用准线方程,顶点坐标,得到![]() 的值,从而得到椭圆方程;(2)①利用等腰直角三角形,求得
的值,从而得到椭圆方程;(2)①利用等腰直角三角形,求得![]() 点坐标;再利用点差法,求得直线
点坐标;再利用点差法,求得直线![]() 的斜率,得到直线方程;②根据点差法得到的结论
的斜率,得到直线方程;②根据点差法得到的结论![]() ,通过假设直线
,通过假设直线![]() 方程,代入椭圆方程,利用韦达定理求得
方程,代入椭圆方程,利用韦达定理求得![]() 两点坐标,构造关于
两点坐标,构造关于![]() 的方程,求得
的方程,求得![]() 的取值。
的取值。
![]() 椭圆C:
椭圆C:![]() 的右准线方程为
的右准线方程为![]() ,右顶点为
,右顶点为![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 椭圆C的方程为
椭圆C的方程为![]() .
.
![]() 为等腰直角三角形且直角顶点P在x轴上方.
为等腰直角三角形且直角顶点P在x轴上方.
![]() 的方程为:
的方程为:![]() ,AP的方程为:
,AP的方程为:![]() .
.
由![]() 可得
可得![]() .
.
设![]() ,
,![]() 则
则![]() ,
,![]()
![]() ,
,![]() ,
,
两式相减可得![]()
可得:![]() ,又
,又![]() ,可得
,可得![]() .
.
![]() 直线MN的方程为
直线MN的方程为![]() ,即
,即![]() .
.
![]() 设AM的斜率为k,
设AM的斜率为k,![]() 点P是线段MN的中点,点Q是线段NA的中点,
点P是线段MN的中点,点Q是线段NA的中点,![]() .
.
![]() 的角平分线与x轴垂直,
的角平分线与x轴垂直,![]() ,
,![]() .
.
由![]() 可得
可得![]() ,
,![]() .
.
设AM的方程为![]() .
.
由![]() 可得
可得![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
以![]() 换k,可得
换k,可得![]() ,
,![]() ,
,
![]() ,
,
整理可得:![]() ,解得
,解得![]() ,
,![]() .
.
![]() 直线AM的斜率为
直线AM的斜率为![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的图象两相邻对称轴之间的距离是
的图象两相邻对称轴之间的距离是![]() ,若将
,若将![]() 的图象向右平移
的图象向右平移![]() 个单位长度,所得图象对应的函数
个单位长度,所得图象对应的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的对称轴及单调增区间;
的对称轴及单调增区间;
(3)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,是奇函数.
,是奇函数.
(1)求实数m的值;
(2)画出函数![]() 的图象,并根据图象求解下列问题;
的图象,并根据图象求解下列问题;
①写出函数![]() 的值域;
的值域;
②若函数![]() 在区间
在区间![]() 上单调递增,求实数a的取值范围.
上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查,6人得分情况为:5,6,7,8,9,10.把这6名学生的得分看成一个总体.
(1)求该总体的平均数;
(2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·衡水二模)某商场在元旦举行购物抽奖促销活动,规定顾客从装有编号0,1,2,3,4的五个相同小球的抽奖箱中一次任意摸出两个小球,若取出的两个小球的编号之和等于7则中一等奖,等于6或5则中二等奖,等于4则中三等奖,其余结果为不中奖.
(1)求中二等奖的概率.
(2)求不中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,![]() 平面ABCD,四边形ABCD为菱形,
平面ABCD,四边形ABCD为菱形,![]() ,点M,N分别在棱FD,ED上.
,点M,N分别在棱FD,ED上.
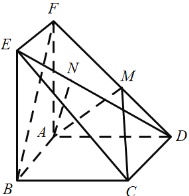
(1)若![]() 平面MAC,设
平面MAC,设![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,平面AEN平面EDC所成的锐二面角为
,平面AEN平面EDC所成的锐二面角为![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com