
分析 (1)甲不在中间也不在两端,先在2个位置安排甲,再安排其它人,可得结论;
(2)甲、乙两人必须排在两端,先在两段安排甲乙,再安排其它人,可得结论;
(3)甲、乙两人不相邻,利用插空法,可得结论;
(4)男、女分别排在一起,利用捆绑法,可得结论;
(5)男女相间排列,利用插空法,可得结论;
(6)甲、乙、丙三人按从左到右的顺序不变,利用除法,可得结论.
解答 解:(1)甲不在中间也不在两端,先在2个位置安排甲,再安排其它人,可得$A_2^1A_4^4=48$------(2分)
(2)甲、乙两人必须排在两端,先在两段安排甲乙,再安排其它人,可得$A_2^2A_3^3=12$------(4分)
(3)甲、乙两人不相邻,利用插空法,可得$A_3^3A_4^2=72$------(6分)
(4)男、女分别排在一起,利用捆绑法,可得$A_3^3A_2^2A_2^2=24$------(8分)
(5)男女相间排列,利用插空法,可得$A_3^3A_2^2=12$------(10分)
(6)甲、乙、丙三人按从左到右的顺序不变,利用除法,可得$\frac{A_5^5}{A_3^3}=20$------(12分)
点评 本题集排列组合的多种类型于一题,充分体现了元素分析法(优先考虑特殊元素)、位置分析法(优先考虑特殊位置)、插空法等常见的解题思路.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:填空题
 如图所示,在三棱锥PABC中,PA⊥平面ABC,D是侧面PBC上的一点,过D作平面ABC的垂线DE,其中D∉PC,则DE与平面PAC的位置关系是平行.
如图所示,在三棱锥PABC中,PA⊥平面ABC,D是侧面PBC上的一点,过D作平面ABC的垂线DE,其中D∉PC,则DE与平面PAC的位置关系是平行.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
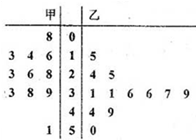 如图是甲、乙两名篮球运动员每场比赛的得分情况的茎叶图$\overline{{x}_{1}}$,$\overline{{x}_{2}}$分别表示甲乙两名运动员每场比赛得分的平均数,s1,s2分别表示甲乙两名运动员每场比赛得分的标准差,则有( )
如图是甲、乙两名篮球运动员每场比赛的得分情况的茎叶图$\overline{{x}_{1}}$,$\overline{{x}_{2}}$分别表示甲乙两名运动员每场比赛得分的平均数,s1,s2分别表示甲乙两名运动员每场比赛得分的标准差,则有( )| A. | $\overline{{x}_{1}}$<$\overline{{x}_{2}}$,s1>s2 | B. | $\overline{{x}_{1}}$<$\overline{{x}_{2}}$,s1<s2 | C. | $\overline{{x}_{1}}$>$\overline{{x}_{2}}$,s1<s2 | D. | $\overline{{x}_{1}}$>$\overline{{x}_{2}}$,s1>s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-1,0) | C. | (0,1) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com