
分析 (1)a=2时,把不等式-3<f(x)<5化为不等式组-3<x2-4x<5,求出解集即可;
(2)由二次函数的图象与性质,讨论a>0时|f(x)|≤5在x∈[0,M(a)]上恒成立时,M(a)最大,此时对应的方程f(x)=±5根的情况,从而求出M(a)的解析式;
(3)f(x)=(x-a)2-a2(t≤x≤t+2),显然f(0)=f(2a)=0,分类讨论,利用y=f(x)在[t,t+2]的最大值为0,最小值是-4,求实数a和t的值.
解答 解:(1)当a=2时,函数f(x)=x2-4x,
∴不等式-3<f(x)<5可化为-3<x2-4x<5,
解得$\left\{\begin{array}{l}{x<1或x>3}\\{-1<x<5}\end{array}\right.$,
∴不等式的解集为(-1,1)∪(3,5);
(2)∵a>0时,f(x)=x2-2ax=(x-a)2-a2,
∴当-a2<-5,即a>$\sqrt{5}$时,
要使|f(x)|≤5在x∈[0,M(a)]上恒成立,
要使得M(a)最大,M(a)只能是x2-2ax=-5的较小的根,
即M(a)=a-$\sqrt{{a}^{2}-5}$;
当-a2≥-5,即0<a≤$\sqrt{5}$时,
要使|f(x)|≤5在x∈[0,M(a)]上恒成立,
要使得M(a)最大,M(a)只能是x2-2ax=5的较大的根,
即M(a)=a+$\sqrt{{a}^{2}+5}$;
综上,M(a)=$\left\{\begin{array}{l}{a-\sqrt{{a}^{2}-5},a>\sqrt{5}}\\{a+\sqrt{{a}^{2}+5},0<a≤\sqrt{5}}\end{array}\right.$.
(3)f(x)=(x-a)2-a2(t≤x≤t+2),显然f(0)=f(2a)=0.
①若t=0,则a≥t+1,且f(x)min=f(a)=-4,或f(x)min=f(2)=-4,
当f(a)=-a2=-4时,a=±2,a=-2不合题意,舍去
当f(2)=4-4a=-4时,a=2,
②若t+2=2a,则a≤t+1,且f(x)min=f(a)=-4,或f(x)min=f(2a-2)=-4,
当f(a)=-a2=-4时,a=±2,若a=2,t=2,符合题意;
若a=-2,则与题设矛盾,不合题意,舍去
当f(2a-2)=-4时,a=2,t=2
综上所述,a=2,t=0和a=2,t=2符合题意.
点评 本题考查了不等式的解法与应用问题,也考查了二次函数的图象与性质的应用问题,是较难理解的题目.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12种 | B. | 13种 | C. | 14种 | D. | 15种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
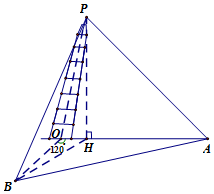 上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求:
上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”.兴趣小组同学实施如下方案来测量塔的倾斜度和塔高:如图,记O点为塔基、P点为塔尖、点P在地面上的射影为点H.在塔身OP射影所在直线上选点A,使仰角k∠HAP=45°,过O点与OA成120°的地面上选B点,使仰角∠HPB=45°(点A、B、O都在同一水平面上),此时测得∠OAB=27°,A与B之间距离为33.6米.试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com