
分析 由柯西不等式,我们易结合a2+b2+c2=1,得到(a+b+$\sqrt{2}$c)2≤(1+1+2)(a2+b2+c2)=4,再由条件可得|x2-1|≥2,解绝对值不等式,即可得到答案.
解答 解:∵(a+b+$\sqrt{2}$c)2≤(1+1+2)(a2+b2+c2)=4,
∴a+b+$\sqrt{2}$c≤2,
又∵a+b+$\sqrt{2}$c≤|x2-1|对于满足条件a2+b2+c2=1的任意实数a,b,c恒成立,
∴|x2-1|≥2,即为x2≥3或x2≤-1,
解得x≤-$\sqrt{3}$或x≥$\sqrt{3}$,
即有实数x的取值范围是(-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞).
点评 本题考查不等式恒成立问题的解法,同时考查柯西不等式的运用,二次不等式的解法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 等于 | B. | 小于 | C. | 大于 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-i | B. | 1+i | C. | -1+i | D. | 1-i |
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:选择题
函数 的定义域为
的定义域为 ,以下命题正确的是( )
,以下命题正确的是( )
①同一坐标系中,函数 与函数
与函数 的图象关于直线
的图象关于直线 对称;
对称;
②函数 的图象既关于点
的图象既关于点 成中心对称,对于任意
成中心对称,对于任意 ,又有
,又有 ,则
,则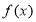 的图象关于直线
的图象关于直线 对称;
对称;
③函数 对于任意
对于任意 ,满足关系式
,满足关系式 ,则函数
,则函数 是奇函数.
是奇函数.
A.①② B.①③ C.②③ D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{7}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{11}$ | D. | $\frac{6}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com