
分析 (1)利用互斥事件概率加法公式和相互独立事件概率乘法公式能求出3名男生能分别求出3名男生中有1名,2名,3名能使账单确认的概率.
(2)由已知得X的可能取值为0,1,2,3,且X~B(3,$\frac{1}{5}$),由此能求出3名女生能使账单确认的人数X的分布列与数学期望.
解答 解:(1)∵3名男生能使账单确认的概率分别为$\frac{1}{4}$,$\frac{1}{5}$,$\frac{1}{6}$,
∴3名男生中有1名能使账单确认的概率:
p1=$\frac{1}{4}(1-\frac{1}{5})(1-\frac{1}{6})$+$(1-\frac{1}{4})•\frac{1}{5}•(1-\frac{1}{6})$+$(1-\frac{1}{4})(1-\frac{1}{5})•\frac{1}{6}$=$\frac{47}{120}$;
3名男生中有2名能使账单确认的概率:
P2=$\frac{1}{4}×\frac{1}{5}×(1-\frac{1}{6})$+$\frac{1}{4}×(1-\frac{1}{5})×\frac{1}{6}$+$(1-\frac{1}{4})×\frac{1}{5}×\frac{1}{6}$=$\frac{1}{10}$,
3名男生都能使账单确认的概率:
p3=$\frac{1}{4}×\frac{1}{5}×\frac{1}{6}$=$\frac{1}{120}$.
(2)由已知得X的可能取值为0,1,2,3,且X~B(3,$\frac{1}{5}$),
P(X=0)=${C}_{3}^{0}(\frac{4}{5})^{3}$=$\frac{64}{125}$,
P(X=1)=${C}_{3}^{1}•\frac{1}{5}(\frac{4}{5})^{2}$=$\frac{48}{125}$,
P(X=2)=${C}_{3}^{2}(\frac{1}{5})^{2}(\frac{4}{5})$=$\frac{12}{125}$,
P(X=3)=${C}_{3}^{3}(\frac{1}{5})^{3}$=$\frac{1}{125}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{64}{125}$ | $\frac{48}{125}$ | $\frac{12}{125}$ | $\frac{1}{125}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
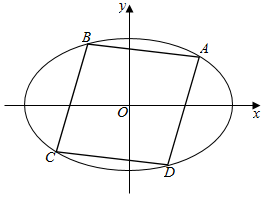 如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.
如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-$\frac{1}{3}$<x<$\frac{1}{2}$} | B. | {x|x<-$\frac{1}{3}$或x>$\frac{1}{2}$} | C. | {x|-$\frac{1}{2}$<x<$\frac{1}{3}$} | D. | {x|x<-$\frac{1}{2}$或x>$\frac{1}{3}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 20 | C. | 21 | D. | 23 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com