
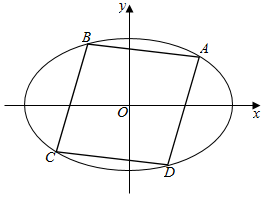
 如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.
如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{4}$+y2=1的所有内接菱形构成的集合为F.分析 (1)设直线AC的方程为y=kx,直线BD的方程为y=-$\frac{1}{k}x$,与椭圆联立,得到OA2=$\frac{4({k}^{2}+1)}{4{k}^{2}+1}$,OB2=$\frac{4({k}^{2}+1)}{{k}^{2}+4}$,由此能求出菱形ABCD的最小面积.
(2)存在定圆${x}^{2}+{y}^{2}=\frac{4}{5}$与F中的菱形都相切,设原点到菱形任一边的距离为d,由当菱形ABCD的对角线在坐标轴上和当菱形ABCD的对角线不在坐标轴上,两种情况证明d=$\frac{2}{\sqrt{5}}$.从而得到存在定圆${x}^{2}+{y}^{2}=\frac{4}{5}$与F中的菱形都相切.
(3)设这条边所在的直线AD的方程为y=t(x-$\sqrt{3}$),由点O(0,0)到直线AD的距离,能求出直线AD的方程.
解答  解:(1)如图,设A(x1,y1),B(x2,y2),
解:(1)如图,设A(x1,y1),B(x2,y2),
当菱形ABCD的对角线在坐标轴上时,其面积为4×$\frac{1}{2}×2×1$=4,
当菱形ABCD的对角线不在坐标轴上时,设直线AC的方程为y=kx,①
则直线BD的方程为y=-$\frac{1}{k}x$,
又椭圆$\frac{{x}^{2}}{4}+{y}^{2}=1$,②
由①②,得${{x}_{1}}^{2}=\frac{4}{4{k}^{2}+1}$,${{y}_{1}}^{2}=\frac{4{k}^{2}}{4{k}^{2}+1}$,
从而$O{A}^{2}={{x}_{1}}^{2}+{{y}_{1}}^{2}$=$\frac{4({k}^{2}+1)}{4{k}^{2}+1}$,
同理可得OB2=${{x}_{2}}^{2}+{{y}_{2}}^{2}$=$\frac{4[(-\frac{1}{k})^{2}+1]}{4(-\frac{1}{k})^{2}+1}$=$\frac{4({k}^{2}+1)}{{k}^{2}+4}$,
∴菱形ABCD的面积为:2×OA×OB=8$\sqrt{\frac{{k}^{4}+2{k}^{2}+1}{4{k}^{4}+17{k}^{2}+4}}$=4$\sqrt{\frac{{k}^{4}+2{k}^{2}+1}{{k}^{4}+\frac{17}{4}{k}^{2}+1}}$
=4$\sqrt{1-\frac{\frac{9}{4}{k}^{2}}{{k}^{4}+\frac{17}{4}{k}^{2}+1}}$=4$\sqrt{1-\frac{9}{4({k}^{2}+\frac{1}{{k}^{2}})+17}}$≥$4\sqrt{1-\frac{9}{4×2\sqrt{{k}^{2}×\frac{1}{{k}^{2}}}+17}}$=$\frac{16}{5}$,
当且仅当k=±1时,等号成立,
综上,得菱形ABCD的最小面积为$\frac{16}{5}$.
(2)存在定圆${x}^{2}+{y}^{2}=\frac{4}{5}$与F中的菱形都相切,设原点到菱形任一边的距离为d,
下证:d=$\frac{2}{\sqrt{5}}$.
证明:由(1)知当菱形ABCD的对角线在坐标轴上时,d=$\frac{2}{\sqrt{5}}$,
当菱形ABCD的对角线不在坐标轴上时,
${d}^{2}=\frac{O{A}^{2}×O{B}^{2}}{O{A}^{2}+O{B}^{2}}$=$\frac{\frac{4({k}^{2}+1)}{4{k}^{2}+1}×\frac{4({k}^{2}+1)}{{k}^{2}+4}}{\frac{4({k}^{2}+1)}{4{k}^{2}+1}+\frac{4({k}^{2}+1)}{{k}^{2}+4}}$
=$\frac{4({k}^{2}+1)^{2}}{({k}^{2}+1)({k}^{2}+4)+({k}^{2}+1)(4{k}^{2}+1)}$
=$\frac{4({k}^{2}+1)^{2}}{({k}^{2}+1)(5{k}^{2}+5)}$=$\frac{4}{5}$,
∴d=$\frac{2}{\sqrt{5}}$.
综上,存在定圆${x}^{2}+{y}^{2}=\frac{4}{5}$与F中的菱形都相切.
(3)设这条边所在的直线AD的方程为y=t(x-$\sqrt{3}$),即tx-y-$\sqrt{3}t$=0,
则点O(0,0)到直线AD的距离为$\frac{|\sqrt{3}t|}{\sqrt{{t}^{2}+1}}=\frac{2}{\sqrt{5}}$,
解得t=$±\frac{2\sqrt{11}}{11}$.
∴直线AD的方程为y=$±\frac{2\sqrt{11}}{11}$(x-$\sqrt{3}$).
点评 本题考查菱形最小面积的求法,考查满足条件的圆是否存在的判断与求法,考查直线方程的求法,是中档题,解题时要认真审题,注意点到直线距离公式、椭圆性质的合理运用.


科目:高中数学 来源: 题型:解答题
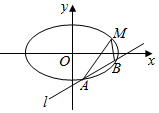 ⑧如图,已知椭圆的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,且经过点M(4,1),直线l:y=x+m交椭圆与A,B两不同的点.
⑧如图,已知椭圆的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{3}}{2}$,且经过点M(4,1),直线l:y=x+m交椭圆与A,B两不同的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com