
一个质地均匀的正方体骰子,其六个面上的点数分别为1、2、3、4、5、6,将这颗骰子连续投掷三次,观察向上的点数,则三次点数依次成等比数列的概率为( )
A.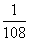 B.
B.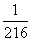
C. D.
D.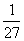
科目:高中数学 来源: 题型:
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中a、b∈{0,1,2,3,4,5},若|a-b|≤1,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
A.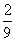 B.
B.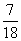
C.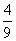 D.
D.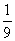
查看答案和解析>>
科目:高中数学 来源: 题型:
一次演出,原计划要排4个节目,因临时有变化,拟再添加2个小品节目,若保持原有4个节目的相对顺序不变,则这6个节目不同的排列方法有( )
A.30种 B.25种
C.24种 D.20种
查看答案和解析>>
科目:高中数学 来源: 题型:
要从5名女生,7名男生中选出5名代表,按下列要求,分别有多少种不同的选法?
(1)至少有1名女生入选;
(2)至多有2名女生入选;
(3)男生甲和女生乙入选;
(4)男生甲和女生乙不能同时入选;
(5)男生甲、女生乙至少有一个人入选.
查看答案和解析>>
科目:高中数学 来源: 题型:
某班将要举行篮球投篮比赛,比赛规则是:每位选手可以选择在A区投篮2次或选择在B区投篮3次.在A区每进一球得2分,不进球得0分;在B区每进一球得3分,不进球得0分,得分高的选手胜出.已知参赛选手甲在A区和B区每次投篮进球的概率分别为 或
或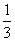 .
.
(1)如果选手甲以在A、B区投篮得分的期望较高者为选择投篮区的标准,问选手甲应该选择在哪个区投篮?
(2)求选手甲在A区投篮得分高于在B区投篮得分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com