
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 正三角形 |
分析 $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$,从而由$\overrightarrow{AB}•(\overrightarrow{AB}-\overrightarrow{AC})=0$得出$\overrightarrow{AB}•\overrightarrow{CB}=0$,这样即可得出AB⊥CB,从而便可得出△ABC的形状.
解答 解:$\overrightarrow{AB}•(\overrightarrow{AB}-\overrightarrow{AC})=\overrightarrow{AB}•\overrightarrow{CB}=0$;
∴$\overrightarrow{AB}⊥\overrightarrow{CB}$;
即AB⊥CB;
∴△ABC是直角三角形.
故选A.
点评 考查向量减法的几何意义,以及向量垂直的充要条件,向量数量积的计算公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | {m|m≥-3} | B. | {m|m≤-3} | C. | {m|m≤2} | D. | {m|m≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
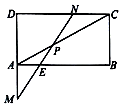 如图,矩形ABCD,AB=2,AD=1,P是对角线AC上一点,$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$,过P的直线分别交DA的延长线,AB,DC于M,E,N,若$\overrightarrow{DM}=m\overrightarrow{DA},\overrightarrow{DN}=n\overrightarrow{DC}$,则2m+3n的最小值是( )
如图,矩形ABCD,AB=2,AD=1,P是对角线AC上一点,$\overrightarrow{AP}=\frac{2}{5}\overrightarrow{AC}$,过P的直线分别交DA的延长线,AB,DC于M,E,N,若$\overrightarrow{DM}=m\overrightarrow{DA},\overrightarrow{DN}=n\overrightarrow{DC}$,则2m+3n的最小值是( )| A. | $\frac{6}{5}$ | B. | $\frac{12}{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -120 | B. | -80 | C. | 80 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com