
分析 (1)设等差数列{an}的公差为d,运用等差数列的通项公式和等比数列中项的性质,解方程可得首项和公差,进而得到所求通项公式;
(2)bn=$\frac{2}{{a}_{n}{a}_{n+1}}$=$\frac{2}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n+1}$,运用数列的求和方法:裂项相消求和,化简整理可得所求和,再解不等式可得n的最小值.
解答 解:(1)设等差数列{an}的公差为d,
a1,a2,a3成等比数列,a3+a4=12,
有$\left\{\begin{array}{l}{{{a}_{2}}^{2}={a}_{1}{a}_{5}}\\{{a}_{3}+{a}_{4}=12}\end{array}\right.$,即$\left\{\begin{array}{l}{({a}_{1}+d)^{2}={a}_{1}({a}_{1}+4d)}\\{2{a}_{1}+5d=12}\end{array}\right.$,
因为d≠0,所以解得a1=1,d=2,
从而{an}的通项公式为an=2n-1,n∈N*.
(2)因为bn=$\frac{2}{{a}_{n}{a}_{n+1}}$=$\frac{2}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n+1}$,
所以前n项和为Sn=1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$
=1-$\frac{1}{2n+1}$,
令1-$\frac{1}{2n+1}$>$\frac{2016}{2017}$,解得n>1008,
故取最小的正整数n为1009.
点评 本题考查等差数列的通项公式和等比数列中项的性质,以及数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
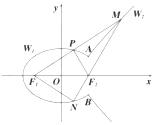 如图:椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)有相同的焦点F1、F2,它们在y轴右侧有两个交点A、B,满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0.将直线AB左侧的椭圆部分(含A,B两点)记为曲线W1,直线AB右侧的双曲线部分(不含A,B两点)记为曲线W2.以F1为端点作一条射线,分别交W1于点P(xP,yP),交W2于点M(xM,yM)(点M在第一象限),设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.
如图:椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)有相同的焦点F1、F2,它们在y轴右侧有两个交点A、B,满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0.将直线AB左侧的椭圆部分(含A,B两点)记为曲线W1,直线AB右侧的双曲线部分(不含A,B两点)记为曲线W2.以F1为端点作一条射线,分别交W1于点P(xP,yP),交W2于点M(xM,yM)(点M在第一象限),设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
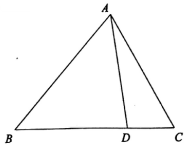 在△ABC中,D为BC边上一点,AD=BD,AC=4,BC=5.
在△ABC中,D为BC边上一点,AD=BD,AC=4,BC=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com