
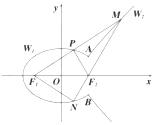
 如图:椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)有相同的焦点F1、F2,它们在y轴右侧有两个交点A、B,满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0.将直线AB左侧的椭圆部分(含A,B两点)记为曲线W1,直线AB右侧的双曲线部分(不含A,B两点)记为曲线W2.以F1为端点作一条射线,分别交W1于点P(xP,yP),交W2于点M(xM,yM)(点M在第一象限),设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.
如图:椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)有相同的焦点F1、F2,它们在y轴右侧有两个交点A、B,满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0.将直线AB左侧的椭圆部分(含A,B两点)记为曲线W1,直线AB右侧的双曲线部分(不含A,B两点)记为曲线W2.以F1为端点作一条射线,分别交W1于点P(xP,yP),交W2于点M(xM,yM)(点M在第一象限),设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.分析 (1)由条件,得F2(1,0),根据$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}=\overrightarrow 0$知,F2、A、B三点共线,且由椭圆与双曲线的对称性知,A、B关于x轴对称,故AB所在直线为x=1,从而得A,B坐标.可得$\frac{1}{a^2}-\frac{1}{{2{b^2}}}=1$,又因为F2为双曲线的焦点,可得a2+b2=1,解出即可得出.
(2)由P(xP,yP)M(xM,yM),得$\overrightarrow{{F_1}P}=({x_P}+1,{y_P})$,$\overrightarrow{{F_1}M}=({x_M}+1,{y_M})$,利用$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.可得xM,yM.由P(xP,yP),M(xM,yM)分别在曲线W1和W2上,代入消去yP得:$3{m^2}{x_P}^2+4m(m-1){x_P}+1-4m=0$(*),将$\frac{1}{m}$代入方程(*),可得xP.从而得到P点坐标.再利用斜率计算公式即可证明.
(3)由(2)知直线PF2与NF2关于x轴对称,结合椭圆的对称性知点P与点N关于x轴对称,可得N坐标.可得$S=\frac{1}{2}×|{F_1}{F_2}|(|{y_M}|+|{y_N}|)$,即可得出.
解答 解:(1)由条件,得F2(1,0),根据$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}=\overrightarrow 0$知,F2、A、B三点共线,
且由椭圆与双曲线的对称性知,A、B关于x轴对称,
故AB所在直线为x=1,从而得$A(1,\frac{{\sqrt{2}}}{2})$,$B(1,-\frac{{\sqrt{2}}}{2})$.
所以,$\frac{1}{a^2}-\frac{1}{{2{b^2}}}=1$,又因为F2为双曲线的焦点,所以a2+b2=1,
解得${a^2}={b^2}=\frac{1}{2}$.
因此,W2的方程为$\frac{x^2}{{\frac{1}{2}}}-\frac{y^2}{{\frac{1}{2}}}=1(x>1)$.
(2)证明:由P(xP,yP)M(xM,yM),得$\overrightarrow{{F_1}P}=({x_P}+1,{y_P})$,$\overrightarrow{{F_1}M}=({x_M}+1,{y_M})$,
由条件,得$\left\{{\begin{array}{l}{{x_M}+1=m({x_P}+1)}\\{{y_M}=m{y_P}}\end{array}}\right.$,即$\left\{{\begin{array}{l}{{x_M}=m{x_P}+m-1}\\{{y_M}=m{y_P}}\end{array}}\right.$,
由P(xP,yP)M(xM,yM)分别在曲线W1和W2上,有,$\left\{{\begin{array}{l}{\frac{{{x_P}^2}}{2}+{y_P}^2=1}\\{2{{(m{x_P}+m-1)}^2}-2{{(m{y_P})}^2}=1}\end{array}}\right.$,消去yP,得,$3{m^2}{x_P}^2+4m(m-1){x_P}+1-4m=0$(*),
将$\frac{1}{m}$代入方程(*),成立,因此(*)有一根${x_P}=\frac{1}{m}$,结合韦达定理得另一根为${x_P}=\frac{1-4m}{3m}$,因为m>1,所以${x_P}=\frac{1-4m}{3m}<-1$,舍去.
所以,${x_P}=\frac{1}{m}$.
从而P点坐标为$(\frac{1}{m},\frac{{\sqrt{{m^2}-\frac{1}{2}}}}{m})$.
所以,直线PF2的斜率${k_{P{F_2}}}=\frac{{\sqrt{{m^2}-\frac{1}{2}}}}{1-m}$,
由xM=mxP+m-1=m,得$M(m,\sqrt{{m^2}-\frac{1}{2}})$.
所以,直线MF2的斜率${k_{M{F_2}}}=\frac{{\sqrt{{m^2}-\frac{1}{2}}}}{m-1}$.
因此,MF2与PF2斜率之和为零.
(3)由(2)知直线PF2与NF2关于x轴对称,结合椭圆的对称性知点P与点N关于x轴对称,故$N(\frac{1}{m},\frac{1}{m}\sqrt{{m^2}-\frac{1}{2}})$,
因此,$S=\frac{1}{2}×|{F_1}{F_2}|(|{y_M}|+|{y_N}|)$=$\frac{1}{2}×2(\sqrt{{m^2}-\frac{1}{2}}+\frac{1}{m}\sqrt{{m^2}-\frac{1}{2}})$,=$\sqrt{{m^2}-\frac{1}{2}}+\sqrt{1-\frac{1}{{2{m^2}}}}$,
因为S在(1,+∞)上单调递增,
所以S的取值范围是$(\sqrt{2},+∞)$.
点评 本题考查了椭圆与双曲线的标准方程及其性质、一元二次方程的根与系数的关系、中点坐标公式、斜率计算公式、三角形面积计算公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB、BB1的中点,AB=BC.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB、BB1的中点,AB=BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2n+41 | B. | -2n+39 | C. | -n2+40n | D. | -n2-40n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com