
分析 (Ⅰ)将a=1代入f(x),得到f(x)的导数,求出函数的单调区间,从而证出f(x)≤0;
(Ⅱ)求出f(x)的导数,通过讨论a的符号,求出函数的单调区间即可;
(Ⅲ)根据lnx<x-1,(x>1),令t=x-1,则x=t+1,得到ln(t+1)<t,(t>0),分别取t=$\frac{1}{2}$,$\frac{1}{4}$,…,$\frac{1}{{2}^{n}}$,得到:ln(1+$\frac{1}{2}$)<$\frac{1}{2}$,ln(1+$\frac{1}{4}$)<$\frac{1}{4}$,…,ln(1+$\frac{1}{{2}^{n}}$)<$\frac{1}{{2}^{n}}$,相加即可.
解答 解:(Ⅰ)证明:a=1时,f(x)=lnx-x+1,
∴f′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$,
当x≥1时,f′(x)≤0,函数f(x)在[1,+∞)递减,即f(x)≤f(1)=0,
当0<x<1时,f′(x)>0,函数f(x)在(0,1)递增,∴f(x)<f(1)=0,
综上,x>0时且a=1时,f(x)≤0;
(Ⅱ)∵f′(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
当a≤0时,f′(x)>0,f(x)在(0,+∞)递增,
当a>0时,f(x)在(0,$\frac{1}{a}$)递增,在($\frac{1}{a}$,+∞)递减;
(Ⅲ)要证(1+$\frac{1}{2}$)(1+$\frac{1}{4}$)…(1+$\frac{1}{{2}^{n}}$)<e,
两边取以e为底的对数,
即只需证ln(1+$\frac{1}{2}$)+ln(1+$\frac{1}{4}$)+…+ln(1+$\frac{1}{{2}^{n}}$)<1,
由(Ⅰ)可得,lnx<x-1,(x>1),令t=x-1,则x=t+1,
∴ln(t+1)<t,(t>0),
分别取t=$\frac{1}{2}$,$\frac{1}{4}$,…,$\frac{1}{{2}^{n}}$,得到:
ln(1+$\frac{1}{2}$)<$\frac{1}{2}$,ln(1+$\frac{1}{4}$)<$\frac{1}{4}$,…,ln(1+$\frac{1}{{2}^{n}}$)<$\frac{1}{{2}^{n}}$,
将上述n个不等式相加,得:
ln(1+$\frac{1}{2}$)+ln(1+$\frac{1}{4}$)+…+ln(1+$\frac{1}{{2}^{n}}$)<$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$<1.
点评 本题考查了导数的应用,考查函数的单调性、最值问题,考查不等式问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
 某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60)内适合投掷相关方面训练,试估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )
某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60)内适合投掷相关方面训练,试估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为( )| A. | 4:3:1 | B. | 5:3:1 | C. | 5:3:2 | D. | 3:2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
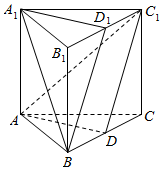 如图所示,正三棱柱ABC-A1B1C1中,A1A=3,AB=2,D是BC上的中点,D1是B1C1的中点,
如图所示,正三棱柱ABC-A1B1C1中,A1A=3,AB=2,D是BC上的中点,D1是B1C1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
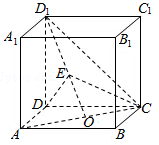 已知正方体ABCD-A1B1C1D1的棱长为2,O是AC的中点,E是线段D1O上一点,且$\overrightarrow{{D_1}E}=λ\overrightarrow{EO}$.
已知正方体ABCD-A1B1C1D1的棱长为2,O是AC的中点,E是线段D1O上一点,且$\overrightarrow{{D_1}E}=λ\overrightarrow{EO}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
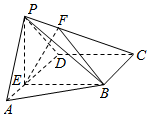 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2$\sqrt{3}$,PA=ED=2AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抛物线 | B. | 椭圆 | C. | 双曲线的右支 | D. | 一条直线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com