
分析 (1)利用任意角的三角函数的定义,求得sinα,cosα,tanα的值.
(2)利用同角三角函数的基本关系,以及三角函数在各个象限中的符号,求得cosα,tanα的值.
解答 解:(1)∵已知角α终边经过点P(-3,-4),∴x=-3,y=4,r=|OP|=5,
∴sinα=$\frac{y}{r}$=$\frac{4}{5}$,cosα=$\frac{x}{r}$=-$\frac{3}{5}$,tanα=$\frac{y}{x}$=-$\frac{4}{3}$的值;
(2)∵已知角α是第二象限角,且$sinα=\frac{3}{5}$,∴cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{4}{5}$,
tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$.
点评 本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2015) | B. | (-∞,-2019) | C. | (-2015,0) | D. | (-2019,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
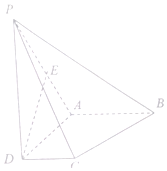 如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.
如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 满意 | 不满意 | 合计 | |
| 男 | 10 | 20 | 30 |
| 女 | 15 | 5 | 20 |
| 合计 | 25 | 25 | 50 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| A. | 有95%的把握认为对电视节目的满意度与性别无关 | |
| B. | 有99%的把握认为对电视节目的满意度与性别无关 | |
| C. | 有99%的把握认为对电视节目的满意度与性别有关 | |
| D. | 有95%的把握认为对电视节目的满意度与性别有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-$\sqrt{3}$]∪[$\sqrt{3}$,2) | B. | [-2,-$\sqrt{3}$)∪($\sqrt{3}$,2] | C. | [-2,2] | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com