
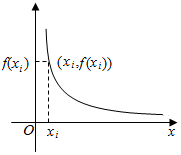 已知函数f(x)=$\frac{1}{x}$(x>0),对于正数x1,x2,…,xn(n∈N+),记Sn=x1+x2+…+xn,如图,由点(0,0),(xi,0),(xi,f(xi)),(0,f(xi))构成的矩形的周长为Ci(i=1,2,…,n),都满足Ci=4Si(i=1,2,…,n).
已知函数f(x)=$\frac{1}{x}$(x>0),对于正数x1,x2,…,xn(n∈N+),记Sn=x1+x2+…+xn,如图,由点(0,0),(xi,0),(xi,f(xi)),(0,f(xi))构成的矩形的周长为Ci(i=1,2,…,n),都满足Ci=4Si(i=1,2,…,n).分析 (Ⅰ)利用矩形的周长公式计算可知$2{S_i}={x_i}+\frac{1}{x_i}$(i=1,2,…,n),进而令i=1计算即得结论;
(Ⅱ)通过(I),分别令i=2、i=3,计算可知${x_2}=\sqrt{2}-1$、${x_3}=\sqrt{3}-\sqrt{2}$,进而由此猜想${x_n}=\sqrt{n}-\sqrt{n-1}$(n∈N+),然后利用数学归纳法证明即可.
解答 (Ⅰ)解:由题意知,${C_i}=2({x_i}+f({x_i}))=2({x_i}+\frac{1}{x_i})$(i=1,2,…,n),
又因为Ci=4Si(i=1,2,…,n),
所以$2{S_i}={x_i}+\frac{1}{x_i}$(i=1,2,…,n).---------------------------------------(1分)
令i=1,得$2{S_1}={x_1}+\frac{1}{x_1}$,
又S1=x1,且x1>0,故x1=1.-------------------------------------(2分)
(Ⅱ)解:令i=2,得$2{S_2}={x_2}+\frac{1}{x_2}$,
又S2=x1+x2,x1=1,且x2>0,故${x_2}=\sqrt{2}-1$;------------------------------------(3分)
令i=3,得$2{S_3}={x_3}+\frac{1}{x_3}$,
又S3=x1+x2+x3,x1=1,${x_2}=\sqrt{2}-1$,且x3>0,故${x_3}=\sqrt{3}-\sqrt{2}$;----------(4分)
由此猜想,${x_n}=\sqrt{n}-\sqrt{n-1}$(n∈N+).----------------------------(5分)
下面用数学归纳法证明:
①当n=1时,x1=1,命题成立;-----------------------------------(6分)
②假设n=k时命题成立,即${x_k}=\sqrt{k}-\sqrt{k-1}$(k∈N+),-----------------------------(7分)
则当n=k+1时,$2{S_{k+1}}={x_{k+1}}+\frac{1}{{{x_{k+1}}}}$,又Sk+1=Sk+xk+1,$2{S_k}={x_k}+\frac{1}{x_k}$,
故$({x_k}+\frac{1}{x_k})+2{x_{k+1}}={x_{k+1}}+\frac{1}{{{x_{k+1}}}}$,
由${x_k}=\sqrt{k}-\sqrt{k-1}$,得$x_{k+1}^2+2\sqrt{k}{x_{k+1}}-1=0$,--------------------------------------(8分)
所以${x_{k+1}}=\sqrt{k+1}-\sqrt{k}$($-\sqrt{k+1}-\sqrt{k}$舍去).-------------------------------------------(9分)
即当n=k+1时命题成立.
综上所述,对任意自然数n,都有${x_n}=\sqrt{n}-\sqrt{n-1}$成立.--------------------------------(10分)
点评 本题考查数学归纳法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27种 | B. | 48种 | C. | 54种 | D. | 72种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.
如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com