
分析 (1)由a4=20,an+1=2an-n+1,可求得a1,a2,a3的值,从而可猜想{an}的一个通项公式.
(2)按照数学归纳法的证题步骤:先证明n=1时命题成立,再假设当n=k时结论成立,去证明当n=k+1时,结论也成立,从而得出命题an=2n+n对任意的正整数n恒成立.
解答 解:(1)∵an+1=2an-n+1,
∴an+1-(n+1)=2(an-n),
当n=3时,a4=2a3-3+1,解得a3=11,
当n=2时,a3=2a2-2+1,解得a2=6,
当n=1时,a2=2a1-1+1,解得a1=3,
可以猜想an=2n+n,
(2)下面用数学归纳法证明:an=2n+n,(n∈N+).
①当n=1时,a1=3,成立,
②假设n=k时成立,即ak=2k+k,
那么当n=k+1时,ak+1=2ak-k+1=2×2k+2k-k+1=2k+1+k+1,
所以当n=k+1时,猜想成立,
由①②可知,猜想成立,即an=2n+n.(n∈N+).
点评 本题考查数学归纳法,考查推理证明的能力,假设n=k(k∈N*)时命题成立,去证明则当n=k+1时,用上归纳假设是关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
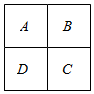 用五种不同的颜色来涂如图所示的田字形区域,要求同一区域上用同一种颜色,相邻区域用不同的颜色(A与C、B与D不相邻).
用五种不同的颜色来涂如图所示的田字形区域,要求同一区域上用同一种颜色,相邻区域用不同的颜色(A与C、B与D不相邻).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
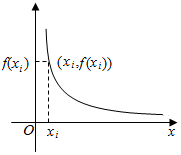 已知函数f(x)=$\frac{1}{x}$(x>0),对于正数x1,x2,…,xn(n∈N+),记Sn=x1+x2+…+xn,如图,由点(0,0),(xi,0),(xi,f(xi)),(0,f(xi))构成的矩形的周长为Ci(i=1,2,…,n),都满足Ci=4Si(i=1,2,…,n).
已知函数f(x)=$\frac{1}{x}$(x>0),对于正数x1,x2,…,xn(n∈N+),记Sn=x1+x2+…+xn,如图,由点(0,0),(xi,0),(xi,f(xi)),(0,f(xi))构成的矩形的周长为Ci(i=1,2,…,n),都满足Ci=4Si(i=1,2,…,n).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com