
分析 分类讨论,确定函数y=|x-3|+a在[0,+∞)上、函数y=2x3-ax2-1在(-∞,0)上零点的个数,即可得出结论.
解答 解:由题意,a≥0时,
x<0,y=2x3-ax2-1,y′=6x2-2ax>0恒成立,
f(x)在(0,+∞)上至多一个零点;
x≥0,函数y=|x-3|+a无零点,
∴a≥0,不符合题意;
-3<a<0时,函数y=|x-3|+a在[0,+∞)上有两个零点,
函数y=2x3-ax2-1在(-∞,0)上无零点,符合题意;
a=-3时,函数y=|x-3|+a在[0,+∞)上有两个零点,
函数y=2x3-ax2-1在(-∞,0)上有零点-1,不符合题意;
a<-3时,函数y=|x-3|+a在[0,+∞)上有两个零点,
函数y=2x3-ax2-1在(-∞,0)上有两个零点,不符合题意;
综上所述,a的取值范围是(-3,0).
故答案为(-3,0).
点评 本题考查函数的零点,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)>eaf(0) | B. | f(a)<eaf(0) | C. | f(a)>f(0) | D. | f(a)<f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
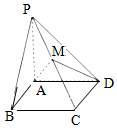 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-2i | B. | 1+2i | C. | -1+2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 份(x) | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 水上狂欢节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com