
分析 求出△ACD的外接圆半径和圆心,根据点与圆的位置关系即可得出BD的最大值.
解答 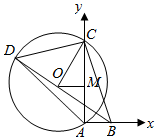 解:设△ACD的外接圆半径为r,则2r=$\frac{AC}{sin∠ADC}$=10,
解:设△ACD的外接圆半径为r,则2r=$\frac{AC}{sin∠ADC}$=10,
∴r=5.
设△ACD的外接圆圆心为O,则O到AC的距离OM=$\sqrt{{r}^{2}-(\frac{AC}{2})^{2}}$=3,
以AB,AC为坐标轴建立空间坐标系,则O(-3,4)或O(3,4),
∵D在圆O上,
∴当圆心为(-3,4),且B,O,D三点共线时,BD取得最大值.
∴|BD|的最大值为|OB|+r=$\sqrt{(-3-1)^{2}+{4}^{2}}$+5=4$\sqrt{2}$+5.
故答案为:4$\sqrt{2}$+5.
点评 本题考查了平面向量在几何中的应用,属于中档题.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.
如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件 | |
| B. | 命题“若随机变量X~N(1,4),P(X≤0)=m,则P(0<X<2)=1-2m”为真命题 | |
| C. | 命题“若x2-3x+2=0,则x=2”的逆否命题为“若x≠2,则x2-3x+2≠0” | |
| D. | 若命题P:?n∈N,2n>1000,则?P:?n∈N,2n>1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 当前襄阳市正在积极创建文明城市,市某交警支队为调查市民文明驾车的情况,在市区某路口随机检测了40辆车的车速.现将所得数据分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),并绘得如图所示的频率分布直方图.
当前襄阳市正在积极创建文明城市,市某交警支队为调查市民文明驾车的情况,在市区某路口随机检测了40辆车的车速.现将所得数据分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),并绘得如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份i | 1 | 2 | 3 | 4 | 5 | 6 |
| 单价xi(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
| 销售量yi(件) | 11 | 10 | 8 | 6 | 5 | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com