Question

5．在等腰梯形ABCD中，已知AB∥DC，AB=2，BC=1，∠ABC=60°，点E和F分别在线段BC和DC上，且$\overrightarrow{BE}$=$\frac{2}{3}$$\overrightarrow{BC}$，$\overrightarrow{DF}$=$\frac{1}{6}$$\overrightarrow{DC}$，则$\overrightarrow{AE}$•$\overrightarrow{AF}$的值为$\frac{29}{18}$．

Answer 1

分析 根据向量数量积的公式和应用，进行运算求解即可．

解答 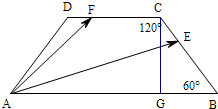解：∵AB=2，BC=1，∠ABC=60°，
∴BG=$\frac{1}{2}BC$=$\frac{1}{2}$，CD=2-1=1，∠BCD=120°，
∵$\overrightarrow{BE}$=$\frac{2}{3}$$\overrightarrow{BC}$，$\overrightarrow{DF}$=$\frac{1}{6}$$\overrightarrow{DC}$，
∴$\overrightarrow{AE}$•$\overrightarrow{AF}$=（$\overrightarrow{AB}$+$\overrightarrow{BE}$）•（$\overrightarrow{AD}$+$\overrightarrow{DF}$）=（$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{BC}$）•（$\overrightarrow{AD}$+$\frac{1}{6}$$\overrightarrow{DC}$）
=$\overrightarrow{AB}$•$\overrightarrow{AD}$+$\frac{1}{6}$$\overrightarrow{AB}$•$\overrightarrow{DC}$+$\frac{2}{3}$$\overrightarrow{BC}$•$\overrightarrow{AD}$+$\frac{2}{3}$$\overrightarrow{BC}$•$\frac{1}{6}$$\overrightarrow{DC}$
=2×1×cos60°+$\frac{1}{6}$×2×1×cos0°+$\frac{2}{3}$×1×1×cos60°+$\frac{2}{3}$×$\frac{1}{6}$×1×1×cos120°
=1+$\frac{1}{3}+\frac{1}{3}-\frac{1}{18}$=$\frac{29}{18}$，
故答案为：$\frac{29}{18}$

点评 本题主要考查向量数量积的应用，根据条件确定向量的长度和夹角是解决本题的关键．