【题目】已知e是自然对数的底数，实数a，b满足eb=2a﹣3，则|2a﹣b﹣1|的最小值为 ．
【答案】3
【解析】解：e是自然对数的底数，实数a，b满足eb=2a﹣3，2a﹣3＞0，可得b=ln（2a﹣3），
|2a﹣b﹣1|=|2a﹣ln（2a﹣3）﹣1|，令2a﹣3=x，上式化为|x﹣lnx+2|，
令y=x﹣lnx+2，可得y′=1﹣ 
，由y′=0，可得x=1，当x∈（0，1）时，y′＜0，函数是减函数，
x＞1时，y′＞0，函数是增函数，x=1时，y=x﹣lnx取得最小值：3．
则|2a﹣b﹣1|的最小值为3．
所以答案是：3．
【考点精析】本题主要考查了函数的最值及其几何意义和利用导数研究函数的单调性的相关知识点，需要掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值；一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减才能正确解答此题．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】双曲线C的中心在原点，右焦点为 
，渐近线方程为 
．
（1）求双曲线C的方程；
（2）设直线l：y=kx+1与双曲线C交于A、B两点，问：当k为何值时，以AB为直径的圆过原点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，AC是⊙O的切线，BC交⊙O于点E． 
（1）若D为AC的中点，证明：DE是⊙O的切线；
（2）若OA= 
CE，求∠ACB的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示，现从这20名学生中随机抽取一人，将“抽出的学生为甲小组学生”记为事件A；“抽出的学生英语口语测试成绩不低于85分”记为事件B．则P（A|B）=（ ）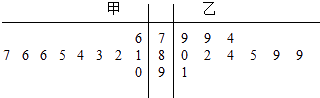
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义：设
为
上的可导函数，若
为增函数，则称
为
上的凸函数.
（1）判断函数
与
是否为凸函数；
（2）设
为
上的凸函数，求证：若
， 
，则
恒有
成立；
（3）设
， 
， 
，求证： 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某企业近3年的前7个月的月利润（单位：百万元）如下面的折线图所示：
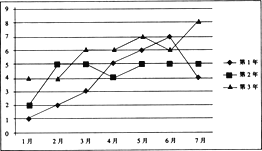
（1）试问这3年的前7个月中哪个月的月平均利润最高？
（2）通过计算判断这3年的前7个月的总利润的发展趋势；
（3）试以第3年的前4个月的数据（如下表），用线性回归的拟合模式估测第3年8月份的利润．
月份x | 1 | 2 | 3 | 4 |
利润y（单位：百万元） | 4 | 4 | 6 | 6 |
相关公式：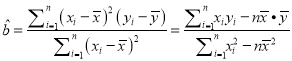 
， 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
.
(1).当
时，求
的单调增区间；
(2)当
，对于任意
，都有
，求实数
的取值范围；
（3）若函数
的图象始终在直线
的下方，求实数的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
