
 —ß–£Œ™≤‚∆¿∞ýº∂—ß…˙∂‘»ŒøŒΩà ¶µƒ¬˙“‚∂»£¨≤…”√°∞100∑÷÷∆°±¥Ú∑÷µƒ∑Ω Ω¿¥º∆∑÷£Æœ÷¥”ƒ≥∞ý—ß…˙÷–Àʪ˙≥È»°10√˚£¨“‘œ¬æ•“∂Õºº«¬º¡ÀÀ˚√«∂‘ƒ≥Ωà ¶µƒ¬˙“‚∂»∑÷ ˝£®“‘ ÆŒª ˝◊÷Œ™æ•£¨∏ˆŒª ˝◊÷Œ™“∂£©£∫
—ß–£Œ™≤‚∆¿∞ýº∂—ß…˙∂‘»ŒøŒΩà ¶µƒ¬˙“‚∂»£¨≤…”√°∞100∑÷÷∆°±¥Ú∑÷µƒ∑Ω Ω¿¥º∆∑÷£Æœ÷¥”ƒ≥∞ý—ß…˙÷–Àʪ˙≥È»°10√˚£¨“‘œ¬æ•“∂Õºº«¬º¡ÀÀ˚√«∂‘ƒ≥Ωà ¶µƒ¬˙“‚∂»∑÷ ˝£®“‘ ÆŒª ˝◊÷Œ™æ•£¨∏ˆŒª ˝◊÷Œ™“∂£©£∫
| ||
|
| ||||
|
| 49 |
| 60 |
| 7 |
| 10 |
| 343 |
| 1000 |
| C | 1 3 |
| 3 |
| 10 |
| 7 |
| 10 |
| 441 |
| 1000 |
| C | 2 3 |
| 3 |
| 10 |
| 7 |
| 10 |
| 189 |
| 1000 |
| 3 |
| 10 |
| 27 |
| 1000 |
| ¶Œ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 343 |
| 1000 |
| 441 |
| 1000 |
| 189 |
| 1000 |
| 27 |
| 1000 |



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫

| A°¢1 | ||
B°¢
| ||
C°¢
| ||
D°¢
|
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
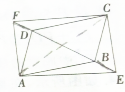
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| m |
| 3 |
| n |
| m |
| n |
| 4 |
| 5 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
| A°¢£®0£¨0£© | ||||||||
B°¢£®
| ||||||||
C°¢£®
| ||||||||
D°¢£®-
|
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| a |
| b |
| a |
| b |
| a |
| b |
| 21 |
| a |
| b |
A°¢
| ||||
| B°¢-5 | ||||
C°¢
| ||||
D°¢-
|
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
|
| 3 |
| 2 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com