
���� ����������ͬ�˦ѵæ�2=2��sin�ȣ������æ�2=x2+y2����sin��=y�ɵ�����C��ֱ�����귽�̣�
���ⷨһ������ȥt�ɵ�ֱ��l����ͨ���̣������D�����꣬�������ߵ����ʣ��ɵ��뾭��Բ��������ֱ֪�ߴ�ֱ��ֱ�߷��̣�����Բ�ķ��������ɵ�x0����������ɵõ�D�����꣮
�ⷨ��������ȥt�ɵ�ֱ��l����ͨ���̣������D��cos�գ�1+sin�գ����ա�[0��2�У������ɵõ�D��ֱ��l�ľ���Ϊd=$2-sin��{��+\frac{��}{3}}��$�����������Ǻ����ĵ�������ֵ�ɵó���
��� �⣺�����ɦ�=2sin�ȣ��ȡ�[0��2�У���
�ɵæ�2=2��sin�ȣ�
�ߦ�2=x2+y2����sin��=y��
������C����ͨ����Ϊx2+y2-2y=0����x2+��y-1��2=1����
���ⷨһ����ֱ�ߵIJ�������Ϊ$\left\{\begin{array}{l}x=\sqrt{3}t+\sqrt{3}\\ y=-3t+2\end{array}\right.$��tΪ������t��R����
��ȥt��ֱ��l����ͨ����Ϊ$y=-\sqrt{3}x+5$��
������C��x2+��y-1��2=1����G��0��1��ΪԲ�ģ�1Ϊ�뾶��Բ��
���D��x0��y0�����ҵ�D��ֱ��l��$y=-\sqrt{3}x+5$�ľ�����̣�
������C�ڵ�D����������ֱ��l��$y=-\sqrt{3}x+5$ƽ�У�
��ֱ��GD��l��б�ʵij˻�����-1����$\frac{{{y_0}-1}}{x_0}����{-\sqrt{3}}��=-1$��
��${x_0}^2+{��{{y_0}-1}��^2}=1$��
�������${x_0}=-\frac{{\sqrt{3}}}{2}$��${x_0}=\frac{{\sqrt{3}}}{2}$��
���D������Ϊ$��-\frac{\sqrt{3}}{2}��\frac{1}{2}��$��$��{\frac{{\sqrt{3}}}{2}��\frac{3}{2}}��$��
���ڵ�D��ֱ��$y=-\sqrt{3}x+5$�ľ�����̣�
��D������Ϊ$��{\frac{{\sqrt{3}}}{2}��\frac{3}{2}}��$��
�ⷨ����ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}x=\sqrt{3}t+\sqrt{3}\\ y=-3t+2\end{array}\right.$��tΪ������t��R����
��ȥt��ֱ��l����ͨ����Ϊ$\sqrt{3}x+y-5=0$��
����Cx2+��y-1��2=1����G��0��1��ΪԲ�ģ�1Ϊ�뾶��Բ��
�ߵ�D������C�ϣ�������D��cos�գ�1+sin�գ����ա�[0��2�У�����
���D��ֱ��l�ľ���Ϊ$d=\frac{{|{\sqrt{3}cos��+sin��-4}|}}{2}$=$2-sin��{��+\frac{��}{3}}��$��
�ߦա�[0��2�У����൱$��=\frac{��}{6}$ʱ��dmin=1��
��ʱD������Ϊ$��{\frac{{\sqrt{3}}}{2}��\frac{3}{2}}��$��
���� ���⿼���˼����귽����ֱ�����귽�̵Ļ�����������������ͨ���̵Ļ��������ֱ�ߵľ��빫ʽ��ֱ����Բ���е����ʡ����ֱ��ֱ��б��֮��Ĺ�ϵ�����Ǻ����ĵ�������ֵ������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{3}$ | B�� | -3 | C�� | $\frac{1}{3}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{\begin{array}{l}x=3cos��\\ y=2sin��\end{array}\right.����������$ | B�� | $\left\{\begin{array}{l}x=2cos��\\ y=3sin��\end{array}\right.����������$ | ||
| C�� | $\left\{\begin{array}{l}x=9cos��\\ y=4sin��\end{array}\right.����������$ | D�� | $\left\{\begin{array}{l}x=4cos��\\ y=9sin��\end{array}\right.����������$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��5�� | B�� | ��-5��1�� | C�� | ��-�ޣ�-1���ȣ�5��+�ޣ� | D�� | ��-�ޣ�-5���ȣ�1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-2���ȣ�3��+�ޣ� | B�� | ��-�ޣ�-2����[1��3�� | C�� | ��-2��1]�ȣ�3��+�ޣ� | D�� | ��-2��1����[1��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
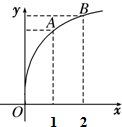 ��֪����f��x����ͼ����ͼ��ʾ��f'��x����f��x���ĵ�������������������ֵf��2��-f��1����f'��1����f'��2����С��������˳��Ϊf�䣨2����f��2��-f��1����f�䣨1����
��֪����f��x����ͼ����ͼ��ʾ��f'��x����f��x���ĵ�������������������ֵf��2��-f��1����f'��1����f'��2����С��������˳��Ϊf�䣨2����f��2��-f��1����f�䣨1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com