
分析 (1)利用《必修四》课本中的定义即可得出.
(2)在直角坐标系xoy中,作单位圆O,以Ox为始边做角α,β,它们的终边分别与单位圆相交于点A,B.则$\overrightarrow{OA}$=(cosα,sinα),$\overrightarrow{OB}$=(cosβ,sinβ).则$\overrightarrow{OA}•\overrightarrow{OB}$=cosαcosβ+sinαsinβ.设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,利用定义可得:$\overrightarrow{OA}•\overrightarrow{OB}$=cosθ.另一方面:由图可知:α-β=2kπ±θ,k∈Z.可得cos(α-β)=cosθ.即可证明.
解答 解:(1)①两个平面向量的夹角的定义:已知两个非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,作$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,则∠AOB=θ(0°≤θ≤180°)叫做向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.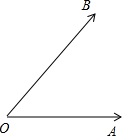
当θ=0°时,$\overrightarrow{a}$与$\overrightarrow{b}$同向;当θ=180°时,$\overrightarrow{a}$与$\overrightarrow{b}$反向.
②两个平面向量数量积的定义:已知两个非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,我们把数量$|\overrightarrow{a}|$$|\overrightarrow{b}|$cosθ叫做向量$\overrightarrow{a}$与$\overrightarrow{b}$的数量积,记作$\overrightarrow{a}•\overrightarrow{b}$,即$\overrightarrow{a}•\overrightarrow{b}$=$|\overrightarrow{a}|$$|\overrightarrow{b}|$cosθ.
其中θ叫做$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.
(2)两角差得余弦公式:cos(α-β)=cosαcosβ+sinαsinβ.
下面给出证明:
在直角坐标系xoy中,作单位圆O,以Ox为始边做角α,β,它们的终边分别与单位圆相交于点A,B.则$\overrightarrow{OA}$=(cosα,sinα),$\overrightarrow{OB}$=(cosβ,sinβ).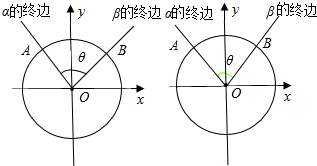
则$\overrightarrow{OA}•\overrightarrow{OB}$=cosαcosβ+sinαsinβ.
设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,
则$\overrightarrow{OA}•\overrightarrow{OB}$=$|\overrightarrow{OA}||\overrightarrow{OB}|$cosθ=cosθ=cosαcosβ+sinαsinβ.
另一方面:由图可知:α=2kπ+β±θ,∴α-β=2kπ±θ,k∈Z.
∴cos(α-β)=cosθ.
∴cos(α-β)=cosαcosβ+sinαsinβ.
点评 本题考查了两个平面向量的夹角的定义、两个平面向量数量积的定义、两角差得余弦公式及其证明、向量数量积的定义及其运算性质,考查了推理能力与计算能力,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{143}$ | B. | $\frac{47}{72}$ | C. | $\frac{3}{79}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高中 | 专科 | 本科 | 研究生 | 合计 | |
| 35岁以下 | 10 | 150 | 50 | 35 | 245 |
| 35-50 | 20 | 100 | 20 | 13 | 153 |
| 50岁以上 | 30 | 60 | 10 | 2 | 102 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0或x<-1} | B. | {x|1<x≤2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:4:5 | B. | 2:$\sqrt{6}$:($\sqrt{3}$+1) | C. | 1:$\sqrt{3}$:2 | D. | 2$\sqrt{2}$:2$\sqrt{3}$:($\sqrt{3}$+$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{8}{17}$ | D. | $-\frac{8}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1008>b1008 | B. | a1008=b1008 | C. | a1008≤b1008 | D. | a1008≥b1008 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com