
【题目】如图,设![]() ,
,![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,
,![]() ,其中正确的命题为( )
,其中正确的命题为( )
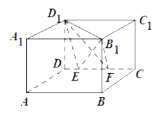
A.三棱锥![]() 的体积为定值
的体积为定值
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.![]() 平面
平面![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
【答案】AD
【解析】
A. 利用![]() ,三棱锥
,三棱锥![]() 的体积为定值,正确
的体积为定值,正确
B. 利用平移法找异面直线所成的角,![]() ,
,![]() 和
和![]() 所成的角为
所成的角为![]() ,所以异面直线
,所以异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,故B错误
,故B错误
C. 若![]() 平面
平面![]() ,则线
,则线![]() 与
与![]() 所成的角为
所成的角为![]() ,而异面直线
,而异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,故C错误
,故C错误
D,建立坐标系,用向量坐标法求解,先求出平面![]() 的一个法向量,再求平面
的一个法向量,再求平面![]() 的一个法向量和
的一个法向量和![]() 的方向向量的夹角,正确
的方向向量的夹角,正确
解:对于A,

故三棱锥![]() 的体积为定值,故A正确
的体积为定值,故A正确
对于B, ![]() ,
,![]() 和
和![]() 所成的角为
所成的角为![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,故B错误
,故B错误
对于C, 若![]() 平面
平面![]() ,则
,则![]() 直线
直线![]() ,即异面直线
,即异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,故C错误
,故C错误
对于D,以![]() 为坐标原点,分布以
为坐标原点,分布以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,则
,则![]() ,
,![]() ,
,![]()
![]()
设平面![]() 的法向量为
的法向量为![]() 则
则
 ,即
,即![]()
令![]() ,则
,则![]()
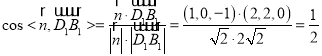
![]()
所以直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,正确
,正确
故选:AD


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点P
,点P![]() 在C上.
在C上.
(1)求椭圆C的方程;
(2)设![]() 分别为椭圆C的左右焦点,过
分别为椭圆C的左右焦点,过![]() 的直线
的直线![]() 与椭圆C交于不同的两点A、B,求△
与椭圆C交于不同的两点A、B,求△![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据中国生态环境部公布的2017年、2018年长江流域水质情况监测数据,得到如下饼图:
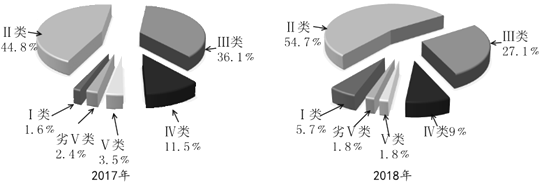
则下列说法错误的是( )
A.2018年的水质情况好于2017年的水质情况
B.2018年与2017年相比较,Ⅰ、Ⅱ类水质的占比明显增加
C.2018年与2017年相比较,占比减小幅度最大的是Ⅳ类水质
D.2018年Ⅰ、Ⅱ类水质的占比超过![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ),且
),且![]() 的解集为
的解集为![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,满足
,满足![]() .
.
(1)求![]() 的值及数列
的值及数列![]() 的通项公式;
的通项公式;
(2)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足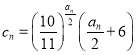 ,若
,若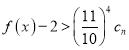 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.

(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内装有大小相同的7个白球和1个黑球.
(1)从口袋内取出3个球,共有多少种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是
A. 三棱锥的四个面可以都是直角三角形;
B. 等差数列{an}的前n项和为Sn(n=1,2,3…),若当首项a1和公差d变化时,a5+a8+a11是一个定值,则S16为定值;
C. ![]() 中,sinA>sinB是
中,sinA>sinB是![]() 的充要条件;
的充要条件;
D. 若双曲线的渐近线互相垂直,则这条双曲线是等轴双曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com