
| A. | x2+y2-3x-2y+1=0 | B. | x2+y2-2x-3y+1=0 | C. | x2+y2-3x-4=0 | D. | x2+y2+x-3y-2=0 |
分析 直接利用A的坐标满足圆的方程,判断求解即可.
解答 解:由题意可知,△ABC的外接圆方程,A的坐标满足圆的方程,
点A(-2,3)代入x2+y2-3x-2y+1=0,左侧=4+9+6-9+1=11≠0,不成立.所以A不正确;
点A(-2,3)代入x2+y2-2x-3y+1=0,左侧=4+9+4-9+1=9≠0,不成立.所以B不正确;
点A(-2,3)代入x2+y2-3x-4=0,左侧=4+9+6-4=15≠0,不成立.所以C不正确;
点A(-2,3)代入x2+y2+x-3y-2=0,左侧=4+9-2-9-2=0,成立.所以D正确;
故选:D.
点评 本题考查直线与圆锥曲线的应用,圆的方程的求法,本题是选择题,方法独特,希望同学们掌握;如果直接求解方法是设出切线的斜率,利用直线与抛物线相切,求出k,然后求出三角形的顶点坐标,利用圆的一般方程求解.


科目:高中数学 来源: 题型:选择题
| A. | x+3y+5=0 | B. | 3x-y-5=0 | C. | 3x+y-1=0 | D. | x-3y-7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三棱柱ABC-A1B1C1中,它的体积是$15\sqrt{3}$,底面△ABC中,∠BAC=90°,AB=4,
三棱柱ABC-A1B1C1中,它的体积是$15\sqrt{3}$,底面△ABC中,∠BAC=90°,AB=4,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校对学生的上学时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,若用分层抽样的方法从该校400名学生中抽取一个容量为20的样本,设m,n表示某两名学生的上学所需时间,且已知m,n∈[40,60)∪[80,100],则事件|m-n|<20的概率为$\frac{2}{5}$.
某校对学生的上学时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,若用分层抽样的方法从该校400名学生中抽取一个容量为20的样本,设m,n表示某两名学生的上学所需时间,且已知m,n∈[40,60)∪[80,100],则事件|m-n|<20的概率为$\frac{2}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
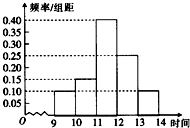 某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )
某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )| A. | 10万元 | B. | 15万元 | C. | 20万元 | D. | 25万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com