
分析 (Ⅰ)由抛物线的几何性质求p的值;
(Ⅱ)设直线的方程为y=2x+t,联立直线方程与抛物线方程,利用消元法得到关于x的一元二次方程,由OA⊥OB得x1x2+y1y2=0,即可求解.
解答 解:(Ⅰ)由抛物线的几何性质知$\frac{2p}{4}=\frac{1}{2}⇒p=1$.…(3分)
(Ⅱ)设直线的方程为y=2x+t.…(4分)
由$\left\{\begin{array}{l}y=2x+t\\{y^2}=2x\end{array}\right.$得4x2+(4t-2)x+t2=0,
由题(4t-2)2-4•4t2>0.解得 $t<\frac{1}{4}$.…(5分)
设A(x1,y1),B(x2,y2),则${x_1}{x_2}=\frac{t^2}{4}$,${({y_1}{y_2})^2}=(2{x_1})(2{x_2})={t^2}$.…(6分)∵$OA⊥OB,\;∴\overrightarrow{OA}•\overrightarrow{OB}=0\;,\;∴{x_1}{x_2}+{y_1}{y_2}=0$.…(8分)
∴$\frac{t^2}{4}±t=0$,解得t=0或-4,4.…(9分)
由题意直线l不过原点且$t<\frac{1}{4}$得t=-4符合题意.…(11分)
所以所求直线方程为y=2x-4.…(12分)
点评 本题主要考查抛物线的应用和抛物线与直线的关系.考查了学生综合分析和解决问题的能力.属于综合题.


科目:高中数学 来源: 题型:解答题
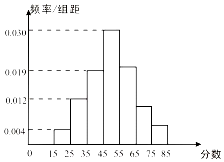 某校1400名学生参加某次知识竞赛,从中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
某校1400名学生参加某次知识竞赛,从中随机抽取100名考生的成绩,绘制成如图所示的频率分布直方图,分数落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com