Question

19．空气质量指数PM2.5（单位：μg/m³）表示每立方米空气中可如肺颗粒物的含量，这个值越高，代表空气污染越严重：

PM2.5日均浓度	0～35	35～75	75～115	115～150	150～250	＞250
空气质量级别	一级	二级	三级	四级	五级	六级
空气质量类别	优	良	轻度污染	中度污染	重度污染	严重污染

甲市2015年2月份中有15对空气质量指数PM2.5进行监测，获得PM2.5日均浓度数据茎叶图如图所示．
（Ⅰ）在15天内任取2天，求甲市空气质量类别均为良的概率；
（Ⅱ）在15天内任取2天，记甲市空气质量级别不超过三级的天数为X，求随机变量X的分布列及数学期望．

Answer 1

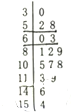
分析 （I）由茎叶图可知：甲市在15天内有4天的空气质量类别为良，利用相互独立事件的概率计算公式即可得出甲市空气质量类别均为良的概率；
（Ⅱ）利用超几何分布即可得到分布列，再利用数学期望的计算公式即可得出．

解答 解：（Ⅰ）由茎叶图知，甲市在15天内有4天的空气质量类别为良，所以P=$\frac{{C}_{4}^{2}}{{C}_{15}^{2}}$=$\frac{2}{35}$；
（Ⅱ）由茎叶图知，甲市在15天内有12天的空气质量级别不超过三级，X的可能取值为0，1，2，
则P（X=0）=$\frac{{C}_{3}^{2}}{{C}_{15}^{2}}$=$\frac{1}{35}$，P（X=1）=$\frac{{C}_{12}^{1}{C}_{3}^{1}}{{C}_{15}^{2}}$=$\frac{12}{35}$，P（X=2）=$\frac{{C}_{12}^{2}}{{C}_{15}^{2}}$=$\frac{22}{35}$．
所以X的分布列为：

X	0	1	2
P	$\frac{1}{35}$	$\frac{12}{35}$	$\frac{22}{35}$

数学期望E（X）=1×$\frac{12}{35}$+2×$\frac{22}{35}$=$\frac{8}{5}$．

点评 正确理解茎叶图、相互独立事件的概率计算公式、超几何分布、随机变量的分布列、数学期望的计算公式、排列与组合的计算公式是解题的关键．