
 如图所示的多面体 ABC-EFGH中,AB∥EG,AC∥EH,且△ABC与△EGH相似,AE⊥平面EFGH,EF=FG=$\sqrt{2},GH=1,EH=\sqrt{5},∠EGH={90°}$,且 AC=$\frac{1}{2}$EH,AE=EG
如图所示的多面体 ABC-EFGH中,AB∥EG,AC∥EH,且△ABC与△EGH相似,AE⊥平面EFGH,EF=FG=$\sqrt{2},GH=1,EH=\sqrt{5},∠EGH={90°}$,且 AC=$\frac{1}{2}$EH,AE=EG分析 (1)取EG的中点O,连结OF、OB,通过线面垂直的判定定理及性质定理即得结论;
(2)以O为原点,以OF、OG、OB所在直线的方向分别为x、y、z轴的正方向建立空间直角坐标系,则所求值即为平面GBF的一个法向量与平面GBH的一个法向量的夹角的余弦值的绝对值的相反数,计算即可.
解答  (1)证明:∵AB∥EG,且△ABC∽△EGH,AC=$\frac{1}{2}$EH,
(1)证明:∵AB∥EG,且△ABC∽△EGH,AC=$\frac{1}{2}$EH,
∴AB=$\frac{1}{2}$EG,
取EG的中点O,连结OF、OB,∴OB∥AE,
又∵AE⊥平面EFGH,∴OB⊥平面EFGH,
又∵EG?平面EFGH,∴OB⊥EG,
又∵EF=FG=$\sqrt{2}$,∴OF⊥EG,
∵OF∩OB=O,∴EG⊥平面OBF,
∵BF?平面OBF,∴BF⊥EG;
(2)解:由(1)知OF、OG、OB两两垂直,
如图,以O为原点,以OF、OG、OB所在直线的方向分别
为x、y、z轴的正方向建立空间直角坐标系,
∵GH=1,EH=$\sqrt{5}$,∠EGH=90°,
∴EG=$\sqrt{E{H}^{2}-1}$=2,
∵EF=FG=$\sqrt{2}$,∴OF=1,
∵AE=EG,∴OB=2,
∴F(1,0,0),G(0,1,0),B(0,0,2),H(-1,1,0),
∴$\overrightarrow{GF}$=(1,-1,0),$\overrightarrow{GB}$=(0,-1,2),$\overrightarrow{GH}$=(-1,0,0),
设平面GBF的一个法向量为$\overrightarrow{n}$=(x1,y1,z1),
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{GF}=0}\\{\overrightarrow{n}•\overrightarrow{GB}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{{x}_{1}-{y}_{1}=0}\\{-{y}_{1}+2{z}_{1}=0}\end{array}\right.$,
令z1=1,得$\overrightarrow{n}$=(2,2,1),
设平面GBH的一个法向量为$\overrightarrow{m}$=(x2,y2,z2),
同理可得$\overrightarrow{m}$=(0,2,1),
∴$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{4+1}{\sqrt{4+4+1}•\sqrt{4+1}}$=$\frac{\sqrt{5}}{3}$,
由图可知,二面角F-BG-H为钝角,
∴其余弦值为$-\frac{\sqrt{5}}{3}$.
点评 本题考查空间线面位置关系的判断及求二面角,考查空间想象能力、运算求解能力及推理论证能力,注意解题方法的积累,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点(0,-1),且离心率为$\frac{{\sqrt{3}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点(0,-1),且离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100].规定90分及其以上为合格.
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100].规定90分及其以上为合格.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

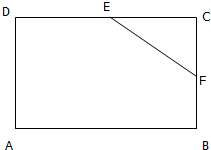
| A. | $\overrightarrow{AE}$•$\overrightarrow{FC}$=0 | B. | $\overrightarrow{AE}$•$\overrightarrow{DF}$>0 | C. | $\overrightarrow{FC}$=$\overrightarrow{FD}$+$\overrightarrow{FB}$ | D. | $\overrightarrow{FD}$•$\overrightarrow{FB}$<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可如肺颗粒物的含量,这个值越高,代表空气污染越严重:| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com