
【题目】在四面体![]() 中,若
中,若![]() ,则当四面体
,则当四面体![]() 的体积最大时其外接球表面积为( )
的体积最大时其外接球表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.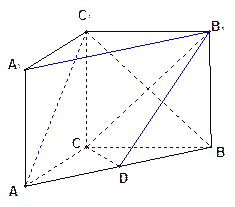
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(Ⅰ)求ω的值和f(x)的单调递增区间;
(Ⅱ)若关于x的方程f(x)﹣m=0在区间[0,![]() ]上有两个实数解,求实数m的取值范围.
]上有两个实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018、2019每高考数学全国Ⅰ卷中,第22题考查坐标系和参数方程,第23题考查不等式选讲.2018年髙考结束后,某校经统计发现:选择第22题的考生较多并且得分率也较高.为研究2019年选做题得分情况,该校高三质量检测的命题完全采用2019年高考选做题模式,在测试结束后,该校数学教师对全校高三学生的选做题得分进行抽样统计,得到两题得分的统计表如下(已知每名学生只选做—道题):
第22题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 50 | 75 | 125 | 200 |
文科人数 | 25 | 25 | 125 | 0 | 25 |
第23题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 30 | 52 | 58 | 60 | 200 |
文科人数 | 5 | 10 | 10 | 5 | 70 |
(1)完成如下2×2列联表,并判断能否有99%的把握认为“选做题的选择”与“文、理科的科类”有关;
选做22题 | 选做23题 | 总计 | |
理科人数 | |||
文科人数 | |||
总计 |
(2)若以全体高三学生选题的平均得分作为决策依据,如果你是考生,根据上面统计数据,你会选做哪道题,并说明理由.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的程序框图中,若输入![]() ,
,![]() ,则输出的
,则输出的![]() 值是( )
值是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/21/1907086498037760/1907898837975040/STEM/25d20caaa911497ea3baaf4f7dee45a3.png]
A. 3 B. 7 C. 11 D. 33
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月(2017年5月到2017年10月)内在西安市的市场占有率进行了统计,并绘制了相应的折线图.
的经营状况,对该公司最近六个月(2017年5月到2017年10月)内在西安市的市场占有率进行了统计,并绘制了相应的折线图.

(1)由拆线图可以看出,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系.求
之间的关系.求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)![]() 公司对员工承诺如果公司的共享单车在2017年年底(12月底)能达到西安市场占有率的
公司对员工承诺如果公司的共享单车在2017年年底(12月底)能达到西安市场占有率的![]() ,员工每人都可以获得年终奖,依据上面计算得到回归方程估计员工是否能得到年终奖.
,员工每人都可以获得年终奖,依据上面计算得到回归方程估计员工是否能得到年终奖.
(参考公式:回归直线方程为![]() ,其中
,其中
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的方程为
的方程为![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
(1)求过点![]() 且与圆
且与圆![]() 相切的直线方程;
相切的直线方程;
(2)过点![]() 任作一条直线
任作一条直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且圆
,且圆![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,求证:直线
,求证:直线![]() 与
与![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com