Question

7．给出下列命题：
①函数y=sin（$\frac{5}{2}$π-x）是偶函数；
②方程lgx=sinx有两个不等的实根；
③点（$\frac{π}{3}$，0）是函数f（x）=sin（2x+$\frac{π}{3}$）是的一个对称中心
④设A、B、C∈（0，$\frac{π}{2}$），且sinA-sinC=sinB，cosA+cosC=cosB，则B-A等于-$\frac{π}{3}$；
以上命题中正确的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 ①根据三角函数的诱导公式以及三角函数的性质进行判断．
②先把方程sinx=lgx实根个数转化为函数y=sinx与函数y=lgx的图象交点个数．画出图象，由图象即可得出结论
③根据三角函数的对称性的性质进行判断．
④利用三角函数的平方关系结合两角和差的正弦公式进行化简即可．

解答 解：①函数y=sin（$\frac{5}{2}$π-x）=cosx是偶函数；故①正确，
②∵方程sinx=lgx实根个数，就是函数y=sinx与函数y=lgx的图象交点个数．
∴作出两个函数的图象如图，
∵sinx≤1，且x=10时，y=lgx=1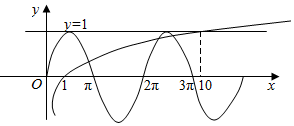

x＞10时，y=lgx＞1．
如图得：交点有3个．
故②错误；
③当x=$\frac{π}{3}$时，f（$\frac{π}{3}$）=sin（2×$\frac{π}{3}$+$\frac{π}{3}$）=sinπ=0，点（$\frac{π}{3}$，0）是函数f（x）=sin（2x+$\frac{π}{3}$）是的一个对称中心，故③正确，
④：∵sinA-sinC=sinB，cosA+cosC=cosB，
∴sinC=sinA-sinB，cosC=cosB-cosA，
又sin²C+cos²C=1，
∴（sinA-sinB）²+（cosB-cosA）²=1，
即sin²A-2sinAsinB+sin²B+cos²B-2cosAcosB+cos²A=1，
整理得：cos（A-B）=cosAcosB+sinAsinB=$\frac{1}{2}$，
在A，B，C∈（0，）内，sinA＞0，sinB＞0，sinC＞0，由题中条件得sinA-sinB=sinC＞0，
又由正弦函数增减性得A＞B，所以A-B＞0，又A，B，C∈（0，$\frac{π}{2}$），
∴0＜A-B＜$\frac{π}{2}$，
则A-B=$\frac{π}{3}$，即B-A=-$\frac{π}{3}$．故④正确，

点评 本题主要考查命题的真假判断，涉及的知识点较多，本题综合性较强，难度较大．