
分析 (1)根据线面垂直及直二面角可得D为BC中点,且BD⊥CD,利用直角三角形的性质求出AD,BD,CD,得出棱锥的底面积和高;
(2)四面体的三个面为到腰直角三角形,一个面为正三角形,分别求出每个面的面积即可.
解答 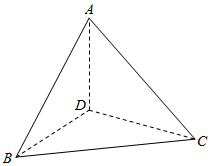 解:(1)∵AD⊥平面BCD,BD?平面BCD,CD?平面BCD,
解:(1)∵AD⊥平面BCD,BD?平面BCD,CD?平面BCD,
∴AD⊥BD,AD⊥CD,
∵Rt△ABC中,AB=AC=1,
∴D是BC的中点,∴BD=CD=AD=$\frac{\sqrt{2}}{2}$.
∴∠BDC为直二面角B-AD-C的平面角,即BD⊥CD.
∴VD-ABC=VA-BCD=$\frac{1}{3}{S}_{△BCD}•AD$=$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{24}$.
(2)∵AD,BD,CD两两垂直,且AD=BD=CD=$\frac{\sqrt{2}}{2}$,
∴S△ABD=S△BCD=S△ACD=$\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}=\frac{1}{4}$.
AB=BC=AC=1.
∴S△ABC=$\frac{\sqrt{3}}{4}×{1}^{2}$=$\frac{\sqrt{3}}{4}$.
∴四面体D-ABC的表面积S=S△ABD+S△BCD+S△ACD+S△ABC=$\frac{3+\sqrt{3}}{4}$.
点评 本题考查了棱锥的体积与表面积计算,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
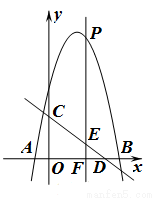
如图,抛物线 与
与 轴交于
轴交于 两点,直线
两点,直线 与
与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,点
,点 是
是 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点 作
作 轴于点
轴于点 ,交直线
,交直线 于点
于点 .设点
.设点 的横坐标为
的横坐标为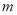 .
.
(1)求抛物线的解析式;
(2)若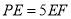 ,求
,求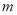 的值;
的值;
(3)若点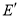 是点
是点 关于直线
关于直线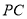 的对称点、是否存在点
的对称点、是否存在点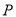 ,使点
,使点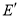 落在
落在 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
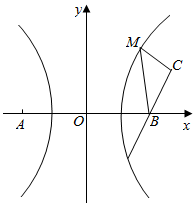 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )| A. | [$\sqrt{26}$+$\sqrt{2}$,+∞) | B. | [$\sqrt{26}$-$2\sqrt{2}$,+∞) | C. | [$\sqrt{26}$-$2\sqrt{2}$,$\sqrt{26}$+$2\sqrt{2}$) | D. | [$\sqrt{26}$-$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com