
【题目】设数列{an}和{bn}的项数均为m,则将数列{an}和{bn}的距离定义为 ![]() |ai﹣bi|.
|ai﹣bi|.
(1)给出数列1,3,5,6和数列2,3,10,7的距离;
(2)设A为满足递推关系an+1= ![]() 的所有数列{an}的集合,{bn}和{cn}为A中的两个元素,且项数均为m,若b1=2,c1=3,{bn}和{cn}的距离小于2016,求m的最大值;
的所有数列{an}的集合,{bn}和{cn}为A中的两个元素,且项数均为m,若b1=2,c1=3,{bn}和{cn}的距离小于2016,求m的最大值;
(3)记S是所有7项数列{an|1≤n≤7,an=0或1}的集合,TS,且T中任何两个元素的距离大于或等于3,证明:T中的元素个数小于或等于16.
【答案】
(1)解:由题意可知,数列1,3,5,6和数列2,3,10,7的距离为1+0+5+1=7
(2)解:设a1=p,其中p≠0,且p≠±1,
由an+1= ![]() ,得a2=
,得a2= ![]() ,a3=﹣
,a3=﹣ ![]() ,a4=
,a4= ![]() ,a5=p,
,a5=p,
∴a1=a5,
因此A中数列的项周期性重复,且间隔4项重复一次,
所数列{bn}中,b4k﹣3=2,b4k﹣2=﹣3,b4k﹣1=﹣ ![]() ,b4k=
,b4k= ![]() ,k∈N*,
,k∈N*,
所以{cn}中,b4k﹣3=3,b4k﹣2=﹣2,b4k﹣1=﹣ ![]() ,b4k=
,b4k= ![]() ,k∈N*,
,k∈N*,
![]() |bi﹣ci|≥
|bi﹣ci|≥ ![]() |bi﹣ci|,得项数m越大,数列{bn}和{cn}的距离越大,
|bi﹣ci|,得项数m越大,数列{bn}和{cn}的距离越大,
由 ![]() =bi﹣ci|=
=bi﹣ci|= ![]() ,
,
得 ![]() |bi﹣ci|=
|bi﹣ci|= ![]() |bi﹣ci|=
|bi﹣ci|= ![]() ×864=2016,
×864=2016,
所以m<3456时, ![]() |bi﹣ci|<2016,
|bi﹣ci|<2016,
故m的最大值为3455
(3)解:证明:假设T中的元素个数大于等于17个,
因为数列{an}中,ai=0或1,
所以仅由数列前三项组成的数组(a1,a2,a3)有且仅有8个,(0,0,0),(1,0,0),(0,1,0),(0,0,1),(1,1,0),
(1,0,1),(0,1,1),(1,1,1),
那么这17个元素(即数列)之中必有三个具有相同的a1,a2,a3,
设这个数列分别为{cn}:c1,c2,c3,c4,c5,c6,c7,{dn}:d1,d2,d3,d4,d5,d6,d7,{fn}:f1,f2,f3,f4,f5,f6,f7,
其中c1=d1=f1,c2=d2=f2,c3=d3=f3,
因为这三个数列中每两个的距离大于等于3,
所以,{bn}和{cn}中,ci=di,(i=4,5,6,7)中至少有三个成立,
不妨设c4≠d4,c5≠d5,c6≠d6,
由题意,c4和d4中一个等于0,而另一个等于1,
又因为f4=0或1,
所以f4=c4和f4=d4中必有一个成立,
同理,得f5=c5和f5=d5中必有一个成立,f6=c6和f6=d6中必有一个成立,
所以“fi=ci(i=3,4,5)中至少有两个成立”或”fi=di(i=4,5,6)中至少有两个成立“中必有一个成立,
所以 ![]() |fi﹣ci|≤2和
|fi﹣ci|≤2和 ![]() |fi﹣di|≤2中必有一个成立.
|fi﹣di|≤2中必有一个成立.
与题意矛盾,
∴T中的元素个数小于或等于16
【解析】(1)由数列距离的定义即可求得数列1,3,5,6和数列2,3,10,7的距离;(2)由数列的递推公式,即可求得a,a3 , a4 , a5 , 求得A中数列的项周期性重复,且间隔4项重复一次,求得数列{bn}和{cn}规律,可知随着项数m越大,数列{bn}和{cn}的距离越大,由 ![]() =bi﹣ci|=
=bi﹣ci|= ![]() ,根据周期的定义,得
,根据周期的定义,得 ![]() |bi﹣ci|=
|bi﹣ci|= ![]() |bi﹣ci|=
|bi﹣ci|= ![]() ×864=2016,求得m的最大值;(3)利用反证法,假设T中的元素个数大于等于17个,设出{cn},{dn},{fn},最总求得
×864=2016,求得m的最大值;(3)利用反证法,假设T中的元素个数大于等于17个,设出{cn},{dn},{fn},最总求得 ![]() |fi﹣ci|≤2和
|fi﹣ci|≤2和 ![]() |fi﹣di|≤2中必有一个成立,与数列的距离大于或等于3矛盾,故可证明T中的元素个数小于或等于16.
|fi﹣di|≤2中必有一个成立,与数列的距离大于或等于3矛盾,故可证明T中的元素个数小于或等于16.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.函数y=f(x)?g(x)的周期为2
B.函数y=f(x)?g(x)的最大值为1
C.将f(x)的图象向左平移 ![]() 个单位后得到g(x)的图象
个单位后得到g(x)的图象
D.将f(x)的图象向右平移 ![]() 个单位后得到g(x)的图象
个单位后得到g(x)的图象
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱台ABC﹣A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6 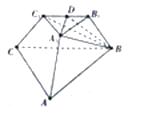
(1)求证:BC1⊥平面AA1C1C
(2)点D是B1C1的中点,求二面角A1﹣BD﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,平面A1ABB1⊥平面ABCD,且∠ABC= ![]() .
. 
(1)求证:BC∥平面AB1C1;
(2)求证:平面A1ABB1⊥平面AB1C1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内的两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数y=f(x)的一对“友好点对”(点对(P,Q)与(Q,P)看作同一对“友好点对”).已知函数f(x)= 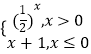 ,则此函数的“友好点对”有( )
,则此函数的“友好点对”有( )
A.3对
B.2对
C.1对
D.0对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间D上的函数f(x)和g(x),如果对任意x∈D,都有|f(x)﹣g(x)|≤1成立,则称f(x)在区间D上可被g(x)替代,D称为“替代区间”.给出以下问题:
①f(x)=x2+1在区间(﹣∞,+∞)上可被g(x)=x2+ ![]() 替代;
替代;
②如果f(x)=lnx在区间[1,e]可被g(x)=x﹣b替代,则﹣2≤b≤2;
③设f(x)=lg(ax2+x)(x∈D1),g(x)=sinx(x∈D1),则存在实数a(a≠0)及区间D1 , D2 , 使得f(x)在区间D1∩D2上被g(x)替代.
其中真命题是( )
A.①②③
B.②③
C.①
D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]()
(1)若曲线C1是一个圆,且点P(1,1)在圆C1外,求实数m的取值范围;
(2)当m=2时,曲线![]() 关于直线x+1=0对称的曲线为
关于直线x+1=0对称的曲线为![]() ,设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线
,设P为平面上的点,满足:存在过P点的无穷多对互相垂直的直线![]() ,它们分别与曲线C1和曲线
,它们分别与曲线C1和曲线![]() 相交,且直线
相交,且直线![]() 被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.求所有满足条件的点P的坐标;
被曲线C1截得的弦长与直线l2被曲线C2截得的弦长总相等.求所有满足条件的点P的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com