
分析 (1)设数列{an}是公差为d的等差数列,运用等差数列的通项公式和求和公式,解方程可得首项和公差,即可得到所求通项;
(2)求出${b_n}={2^{a_n}}$=4n,运用等比数列的求和公式,化简计算即可得到所求和.
解答 解:(1)设数列{an}是公差为d的等差数列,
$\left\{{\begin{array}{l}{{a_3}=6}\\{{S_3}=12}\end{array}⇒\left\{{\begin{array}{l}{{a_1}+2d=6}\\{3{a_1}+3d=12}\end{array}⇒\left\{{\begin{array}{l}{{a_1}=2}\\{d=2}\end{array}}\right.}\right.}\right.⇒{a_n}=2n$;
(2)${b_n}={2^{a_n}}={2^{2n}}={4^n}$,
可得Tn=b1+b2+b3+…+bn=4+42+43+…+4n
=$\frac{{4-4×{4^n}}}{1-4}=\frac{{{4^{n+1}}-4}}{3}$.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查方程思想和运算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 126 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1+\frac{7}{5}i$ | B. | $\frac{1}{5}+\frac{7}{5}i$ | C. | $\frac{1}{3}-\frac{7}{3}i$ | D. | $\frac{5}{3}-\frac{7}{3}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $lg\frac{3}{n+3}$ | B. | $lg\frac{2}{n}$ | C. | $lg\frac{{3({n+1})}}{n+3}$ | D. | $lg\frac{{2({n+2})}}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
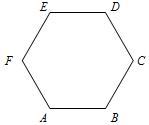 如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.
如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com