
【题目】【2017衡阳第二次联考】已知四棱锥![]() 中,底面为矩形,
中,底面为矩形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 上一点,
上一点, ![]() 为
为![]() 的中点.
的中点.
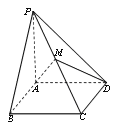
(1)在图中作出平面![]() 与
与![]() 的交点
的交点![]() ,并指出点
,并指出点![]() 所在位置(不要求给出理由);
所在位置(不要求给出理由);
(2)求平面![]() 将四棱锥
将四棱锥![]() 分成上下两部分的体积比.
分成上下两部分的体积比.
 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】从装有![]() 个红球和
个红球和![]() 个黒球的口袋内任取
个黒球的口袋内任取![]() 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
A.至少有一个黒球与都是黒球
B.至少有一个黑球与都是红球
C.至少有一个黒球与至少有![]() 个红球
个红球
D.恰有![]() 个黒球与恰有
个黒球与恰有![]() 个黒球
个黒球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017省息一中第七次适应性考】已知函数![]() (
(![]() ),且
),且![]() 的导数为
的导数为![]() .
.
(Ⅰ)若![]() 是定义域内的增函数,求实数
是定义域内的增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若方程![]() 有3个不同的实数根,求实数
有3个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ax﹣2,g(x)=a(x﹣2a)(x+2﹣a),a∈R且a≠0.
(1)若{x|f(x)g(x)=0}={1,2},求实数a的值;
(2)若{x|f(x)<0或g(x)<0}=R,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com