
| A. | 1 | B. | 2 | C. | -1 | D. | -$\frac{1}{2}$ |
分析 作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到a的值.
解答 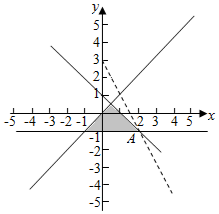 解:不等式组$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤a}\\{y≥-1}\end{array}\right.$对应的平面区域如图:
解:不等式组$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤a}\\{y≥-1}\end{array}\right.$对应的平面区域如图:
由z=2x+y得y=-2x+z,
平移直线y=-2x+z,则由图象可知当直线y=-2x+z经过点A时直线y=-2x+z的截距最大,
此时z最大,为2x+y=16
由$\left\{\begin{array}{l}{2x+y=3}\\{y=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,即A(2,-1),
此时点A在x+y=a,
即2-1=a,
解得a=1,
故选:A.
点评 本题主要考查线性规划的应用,根据z的几何意义,利用数形结合是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x≤0} | B. | {x|-1<x<3} | C. | {x|0<x<3} | D. | {x|x≤0或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙两厂生产的一批零件尺寸服从N(5,0.12),如果零件尺寸在(μ-3σ,μ+3σ)以外,我们就有理由认为生产中可能出现了异常情况.现从甲、乙两厂各抽取10件零件检测,尺寸如茎叶图所示:则以下判断正确的是( )
甲、乙两厂生产的一批零件尺寸服从N(5,0.12),如果零件尺寸在(μ-3σ,μ+3σ)以外,我们就有理由认为生产中可能出现了异常情况.现从甲、乙两厂各抽取10件零件检测,尺寸如茎叶图所示:则以下判断正确的是( )| A. | 甲、乙两厂生产都出现异常 | B. | 甲、乙两厂生产都正常 | ||
| C. | 甲厂生产正常,乙厂出现异常 | D. | 甲厂生产出现异常,乙厂正常 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
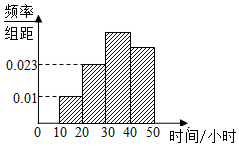 为了了解学生参加体育锻炼的情况,现抽取了n名学生进行调查,结果显示这些学生每月的锻炼时间(单位:小时)都在[10,50],其中锻炼时间在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了了解学生参加体育锻炼的情况,现抽取了n名学生进行调查,结果显示这些学生每月的锻炼时间(单位:小时)都在[10,50],其中锻炼时间在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )| A. | 150 | B. | 160 | C. | 180 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com