
分析 把二次函数配方,然后对a分类讨论,利用函数的单调性求得g(x)的最大值h(a).
解答 解:g(x)=-$\frac{1}{2}$x2-x+2=$-\frac{1}{2}(x+1)^{2}+\frac{5}{2}$,
当a≥-1时,g(x)在[a,a+1]上单调递减,g(x)max=g(a)=$-\frac{{a}^{2}}{2}-a+2$;
当a+1≤-1,即a≤-2时,g(x)在[a,a+1]上单调递增,g(x)max=g(a+1)=$-\frac{{a}^{2}}{2}-2a+\frac{1}{2}$;
当-2<a<-1时,g(x)在[a,-1]上单调递增,在[-1,a]上单调递减,$g(x)_{max}=g(-1)=\frac{5}{2}$.
∴$h(a)=\left\{\begin{array}{l}{-\frac{{a}^{2}}{2}-2a+\frac{1}{2},a≤-2}\\{\frac{5}{2},-2<a<-1}\\{-\frac{{a}^{2}}{2}-a+2,a≥-1}\end{array}\right.$.
点评 本题考查二次函数在闭区间上的最值,考查了分类讨论的数学思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 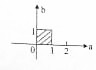 | B. | 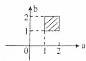 | C. |  | D. | 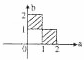 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 26 | C. | 35 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | [-1,1) | D. | (-∞,-1]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
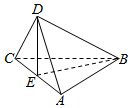 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )| A. | 直线AB⊥直线CD,且直线AC⊥直线BD | |
| B. | 直线AB⊥平面BCD,且直线AC⊥平面BDE | |
| C. | 平面ABC⊥平面BDE,且平面ACD⊥BDE | |
| D. | 平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com