
| A. | 1020 | B. | 1024 | C. | 2044 | D. | 4092 |
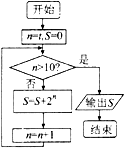
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变量S的值并输出,模拟程序的运行,对程序运行过程中各变量的值进行分析,不难得到输出结果.
解答 解:模拟程序的运行,可得
n=2,S=0
不满足条件n>10,第1次执行循环体,S=22=4,n=3
不满足条件n>10,第2次执行循环体,S=22+23=12,n=4
…
不满足条件n>10,第9次执行循环体,S=22+23+…+210=$\frac{4(1-{2}^{9})}{1-2}$=4(29-1)=2044,n=11
满足条件n>10,退出循环,输出S=2044.
故选:C.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,0) | C. | (0,2) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com