
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{3\sqrt{2}}{8}$ |
分析 以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,利用向量法能求出直线AE与CD所成角的余弦值.
解答 解: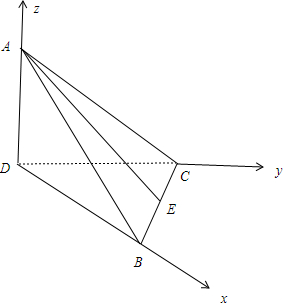 以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,
以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,
A(0,0,1),B(1,0,0),C(0,1,0),E($\frac{1}{2},\frac{1}{2}$,0),D(0,0,0),
$\overrightarrow{AE}$=($\frac{1}{2},\frac{1}{2}$,-1),$\overrightarrow{CD}$=(0,-1,0),
设直线AE与CD所成角为θ,
则直线AE与CD所成角的余弦值为:
cosθ=$\frac{|\overrightarrow{AE}•\overrightarrow{CD}|}{|\overrightarrow{AE}|•|\overrightarrow{CD}|}$=$\frac{\frac{1}{2}}{\sqrt{\frac{6}{4}}}$=$\frac{\sqrt{6}}{6}$.
故选:C.
点评 本题考查异面直线所成角的大小的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
 某市重点中学奥数培训班共有15人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,甲组学生成绩的极差是m,乙组学生成绩的中位数是86,则m+n的值是21.
某市重点中学奥数培训班共有15人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,甲组学生成绩的极差是m,乙组学生成绩的中位数是86,则m+n的值是21.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p:3 为偶数,q:4 为奇数 | B. | p:π<3,q:5>3 | ||
| C. | p:a∈{a,b},q:{a}⊆{a,b} | D. | p:Q⊆R,q:N=Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com