
分析 当直线经过原点时,斜率为-$\frac{3}{4}$,可得要求的直线方程.当直线不经过原点时,设要求的直线方程为x±y=k,再把点(4,-3)代入求得k的值,可得要求的直线方程,综合可得结论.
解答 解:当直线经过原点时,斜率为$\frac{-3-0}{4-0}$=$-\frac{3}{4}$,要求的直线方程为y=-$\frac{3}{4}$x,即3x+4y=0.
当直线不经过原点时,设要求的直线方程为x±y=k,再把点(4,-3)代入可得4-3=k,或4+3=k,
求得k=1,或k=7,故要求的直线方程为x+y-1=0,或x-y-7=0.
综上可得,要求的直线方程为 3x+4y=0、x-y-7=0,或x+y-1=0,
故答案为:3x+4y=0、x-y-7=0,或x+y-1=0,
点评 本题主要考查求直线的方程,体现了分类讨论的数学思想,属于基础题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )
如图所示是南京青奥会传递火炬时,火炬离主会场距离(y)与传递时间(x)之间的函数关系的图象,若用黑点表示主会场的位置,则火炬传递的路线可能是( )| A. |  | B. |  | C. | 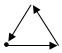 | D. | 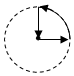 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com