Question

18．已知圆O：x²+y²=1，圆M：（x-a）²+（y-a+4）²=1．若圆M上存在点P，过点P作圆O的两条切线，切点为A，B，使得∠APB=60°，则实数a的取值范围为[$2-\frac{\sqrt{2}}{2}，2+\frac{\sqrt{2}}{2}$]．

Answer 1

分析 由题意画出图形，利用两点间的距离关系求出OP的距离，再由题意得到关于a的不等式求得答案．

解答 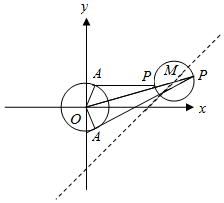解：如图
圆O的半径为1，圆M上存在点P，过点P作圆O的两条切线，切点为A，B，使得∠APB=60°，
则∠APO=30°，在Rt△PAO中，PO=2，
又圆M的半径等于1，圆心坐标M（a，a-4）
∴|PO|_min=|MO|-1，|PO|_max=|MO|+1，
∵$|MO|=\sqrt{{a}^{2}+（a-4）^{2}}$，
∴由$\sqrt{{a}^{2}+（a-4）^{2}}-1≤2≤\sqrt{{a}^{2}+（a-4）^{2}}+1$，解得：2$-\frac{\sqrt{2}}{2}≤a≤2+\frac{\sqrt{2}}{2}$．
故答案为：[$2-\frac{\sqrt{2}}{2}，2+\frac{\sqrt{2}}{2}$]

点评 本题主要考查直线和圆的位置关系的应用，利用数形结合将条件进行等价转化是解决本题的关键，是中档题．