
分析 首先将x分母有理化可得:x=$\sqrt{5}-\sqrt{2}$,又由 $\sqrt{2}$=$\frac{\sqrt{2}}{3}$( $\sqrt{5}$-$\sqrt{2}$)( $\sqrt{5}$+$\sqrt{2}$),然后将其变形求解即可.
解答 解:∵$x=\frac{3}{{\sqrt{5}+\sqrt{2}}}$=$\sqrt{5}-\sqrt{2}$,
∴$\sqrt{2}$=$\frac{\sqrt{2}}{3}$( $\sqrt{5}$-$\sqrt{2}$)( $\sqrt{5}$+$\sqrt{2}$)=$\frac{1}{3}$( $\sqrt{5}$-$\sqrt{2}$)(2+$\sqrt{10}$),
=$\frac{1}{6}$( $\sqrt{5}$-$\sqrt{2}$)(4+2 $\sqrt{10}$),
=-$\frac{1}{6}$( $\sqrt{5}$-$\sqrt{2}$)[( $\sqrt{5}$-$\sqrt{2}$)2-11],
=-$\frac{1}{6}$( $\sqrt{5}$-$\sqrt{2}$)3+$\frac{11}{6}$( $\sqrt{5}$-$\sqrt{2}$),
=-$\frac{1}{6}$x3+$\frac{11}{6}$x.
故答案为:$-\frac{1}{6}{x^3}+\frac{11}{6}x$.
点评 此题考查了分母有理化的知识与平方差公式的应用.题目难度较大,解题是要熟练应用公式与法则.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<-$\frac{1}{2}$,或2<x<3} | B. | {x|2<x<3} | ||
| C. | {x|-$\frac{1}{2}$<x<2} | D. | {x|-1<x<-$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
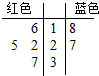 袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示:
袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=16x | B. | y2=8x | C. | y2=-16x | D. | y2=-8x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
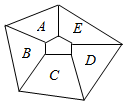 如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )
如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )| A. | 21 | B. | 24 | C. | 30 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com