
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
 |
| y |
 |
| b |
 |
| a |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
. |
| x |
. |
| y |
 |
| b |
| |||||||
|
 |
| a |
 |
| y |
 |
| b |
 |
| a |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
. |
| x |
| 1 |
| 5 |
| 5 |
 |
| i=1 |
. |
| y |
| 1 |
| 5 |
| 5 |
 |
| i=1 |
| ? |
| b |
| |||||||
|
| 112-5×4×5 |
| 90-5×42 |
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
| ? |
| y |
| ? |
| b |
| ? |
| y |


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
|
| A、m∈R | B、m>1 |
| C、m>0 | D、0<m<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(-∞,2ln2-2] |
| B、[2ln2-2,+∞) |
| C、[2ln2,+∞) |
| D、[2ln2-2,2ln2] |
查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| x |
. |
| y |
| A、①② | B、②④ | C、①③ | D、③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:
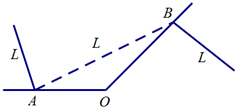 如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.
如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.查看答案和解析>>
科目:高中数学 来源: 题型:
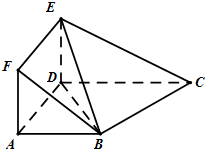 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,查看答案和解析>>
科目:高中数学 来源: 题型:
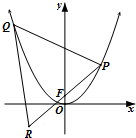 已知抛物线C:y=ax2,直线y=x+
已知抛物线C:y=ax2,直线y=x+| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com