
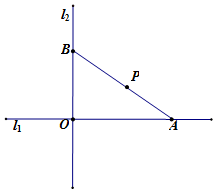
 如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点.
如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点. 分析 以l1为x轴,l2为y轴,建立平面直角坐标系,则O(0,0),P(3,2).
(1)由∠BAO=45°,知OA=OB,可设A(a,0),B(0,a)(a>0),可得直线l的方程为:$\frac{x}{a}+\frac{y}{a}=1$,由l过点P(3,2),代入方程解得a即可得出.
(2)设A(a,0),B(0,b)(a>0,b>0).直线l的方程为:$\frac{x}{a}+\frac{y}{b}=1$,由l过点P(3,2),可得$\frac{3}{a}+\frac{2}{b}=1,b=\frac{2a}{a-3}$,(a>3).从而${S_{△ABO}}=\frac{1}{2}a•b=\frac{1}{2}a•\frac{2a}{a-3}=\frac{a^2}{a-3}$,令a-3=t,t>0,则a2=(t+3)2=t2+6t+9,代入利用函数的单调性即可得出.
解答 解:以l1为x轴,l2为y轴,建立平面直角坐标系,则O(0,0),P(3,2)…(1分)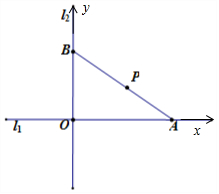
(1)由∠BAO=45°,知OA=OB,可设A(a,0),B(0,a)(a>0)
直线l的方程为:$\frac{x}{a}+\frac{y}{a}=1$,…(3分)
∵l过点P(3,2),∴$\frac{3}{a}+\frac{2}{a}=1⇒a=5$…(5分)
即OA=5(千米) …(7分)
(2)设A(a,0),B(0,b)(a>0,b>0)
则直线l的方程为:$\frac{x}{a}+\frac{y}{b}=1$,
∵l过点P(3,2),∴$\frac{3}{a}+\frac{2}{b}=1,b=\frac{2a}{a-3}$,(a>3)…(9分)
从而${S_{△ABO}}=\frac{1}{2}a•b=\frac{1}{2}a•\frac{2a}{a-3}=\frac{a^2}{a-3}$,…(11分)
令a-3=t,t>0,则a2=(t+3)2=t2+6t+9,
故有${S_{△ABO}}=\frac{{{t^2}+6t+9}}{t}=t+\frac{9}{t}+6$(t>0)
设$f(t)=t+\frac{9}{t}+6$,可证f(t)在(0,3)上递减,在(3,+∞)上递增.
∴当t=3时,f(t)max=f(3)=12…(15分)
此时a=6,b=4,直线l的方程为$\frac{x}{6}+\frac{y}{4}=1$
即OA=6(千米),即OB=4(千米). …(16分)
点评 本题考查了直线的截距式、三角形面积计算公式、函数的单调性、换元方法,考查了推理能力与计算能力,属于中档题.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
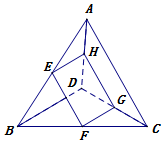 如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA上的中点.
如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA上的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{8i}{5}$ | B. | $\frac{8i}{5}$ | C. | $-\frac{6}{5}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({-\frac{3}{2}})>f({{a^2}+2a+\frac{5}{2}})$ | B. | $f({-\frac{3}{2}})<f({{a^2}+2a+\frac{5}{2}})$ | C. | $f({-\frac{3}{2}})≥f({{a^2}+2a+\frac{5}{2}})$ | D. | $f({-\frac{3}{2}})≤f({{a^2}+2a+\frac{5}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com