
分析 (1)求出函数f(x)的导数,可得切线的斜率,结合已知切线方程,可得a的值;
(2)求出f(x)的导数,可得g(x)的解析式和导数,讨论a=0,a>0,分0<a≤1,a>1,求出单调区间和极值、最值,结合零点存在定理,即可得到a的范围.
解答 解:(1)函数$f(x)=\frac{1}{2}{x^2}+acosx$,
f′(x)=x-asinx,f′($\frac{π}{2}$)=$\frac{π}{2}$-a=$\frac{π+2}{2}$,
所以a=-1,经验证a=-1合题意;
(2)g(x)=f′(x)=x-asinx,g′(x)=1-acosx,
①当a=0时,f(x)=$\frac{1}{2}$x2,显然在x=0时取得最小值,∴a=0合题意;
②当a>0时,
(i)当$\frac{1}{a}$≥1即0<a≤1时,g′(x)≥0恒成立,
∴g(x)在(-∞,+∞)上单调递增,又g(0)=0,
∴当x<0时,g(x)<0 即f′(x)<0,当x>0时,g(x)>0 即f′(x)>0
∴f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增;
∴f(x) 在x=0时取得最小值,
∴当0<a≤1时合题意;
(ii)当0<$\frac{1}{a}$<1即a>1时,在(0,π)内存在唯一x0=arccos$\frac{1}{a}$使g′(x)=0,
当x∈(0,x0)时,∵y=cosx在(0,π)上是单调递减的,∴cosx>cosx0=$\frac{1}{a}$,
∴g′(x)=a ($\frac{1}{a}$-cosx)<0,∴g(x) 在(0,x0)上单调递减,∴g(x)<g(0)=0.
即f′(x)<0,∴f(x)在(0,x0)内单调递减;
∴x∈(0,x0)时,f(x)<0 这与f(x)在x=0时取得最小值即f(x)≥f(0)矛盾,
∴当a>1时不合题意;
综上,a的取值范围是[0,1].
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查分类讨论思想方法以及方程思想、转化思想,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{3}$,0] | B. | (-∞,0)∪[$\frac{2}{3}$,+∞) | C. | [0,$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$]∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人数 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
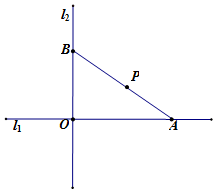 如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点.
如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
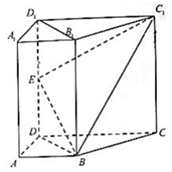 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com