
分析 根据正弦、余弦函数的奇偶性、对称性和单调性,进行求解即可.
解答 解:∵f(x)=sin(ωx+φ)是R上的偶函数,0≤φ≤π,
∴φ=$\frac{π}{2}$,
∴f(x)=sin(ωx+$\frac{π}{2}$)=cosωx;
又f(x)图象关于点M($\frac{3π}{4}$,0)对称,
∴f($\frac{3π}{4}$)=cos($\frac{3π}{4}$ω)=0,
即$\frac{3π}{4}$ω=$\frac{π}{2}$+kπ,k∈Z,
即ω=$\frac{2}{3}$+$\frac{4}{3}$k,k∈Z;
又f(x)在区间[0,$\frac{π}{2}$]上是单调函数,
∴$\frac{T}{2}$≥$\frac{π}{2}$,即$\frac{π}{ω}$≥$\frac{π}{2}$,
解得0<ω≤2;
当k=0时,ω=$\frac{2}{3}$,
当k=1时,ω=2,
∴ω的值为$\frac{2}{3}$或2.
故答案为:$\frac{2}{3}$或2.
点评 本题主要考查了三角函数的图象与性质的应用问题,利用三角函数的单调性、奇偶性和对称性是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | ∅ | C. | [0,10] | D. | (0,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使得$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | 已知随机变量ξ服从正态分布N(1,σ2),若P(ξ≤4)=0.79,则P(ξ≤-2)=0.21 | |
| C. | “φ=$\frac{3π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 | |
| D. | 函数y=f(1+x)与函数y=f(1-x)的图象关于直线x=1对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
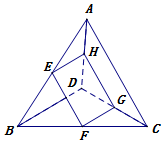 如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA上的中点.
如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA上的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com