
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 设直线l的方程,代入抛物线方程,利用韦达定理及向量数量积的坐标运算,分别求得A和B点横坐标,根据抛物线的焦半径公式,即可求得则|AF|-|BF|.
解答 解:抛物线y2=4x的焦点为F(1,0),假设直线AN的斜率k存在,设AB方程为:y=k(x-1),
$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,整理得:k2x2-2(k2+2)x+k2=0
设两交点为A(x2,y2),B(x1,y1),
∵$\overrightarrow{NB}•\overrightarrow{AB}=0$,则∠NBF=90°,
∴(x1-1)(x1+1)+y12=0,
∴x12+y12=1,∴x12+4x1-1=0(x1>0),∴x1=-2+$\sqrt{5}$,
∵x1x2=1,∴x2=2+$\sqrt{5}$,
∴|AF|-|BF|=(x2+1)-(x1+1)=4,
故选C.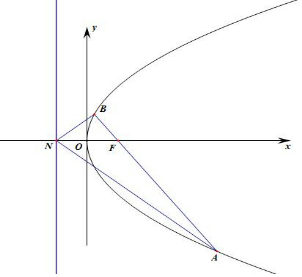
点评 本题考查直线与抛物线的位置关系,考查抛物线的定义,考查学生分析解决问题的能力,属于中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
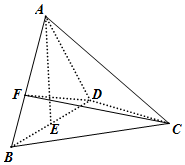 如图,在三棱锥A-BCD中,已知△ABD,△BCD都是边长为2的等边三角形,E为BD中点,且AE⊥平面BCD,F为线段AB上一动点,记$\frac{BF}{BA}=λ$.
如图,在三棱锥A-BCD中,已知△ABD,△BCD都是边长为2的等边三角形,E为BD中点,且AE⊥平面BCD,F为线段AB上一动点,记$\frac{BF}{BA}=λ$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{3}$,0] | B. | (-∞,0)∪[$\frac{2}{3}$,+∞) | C. | [0,$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$]∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
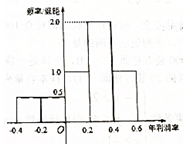 某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.
某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过本地养鱼场年利润率的调研,得到如图所示年利润率的频率分布直方图.对远洋捕捞队的调研结果是:年利润率为60%的可能性为0.6,不赔不赚的可能性为0.2,亏损30%的可能性为0.2.假设该公司投资本地养鱼场的资金为x(x≥0)千万元,投资远洋捕捞队的资金为y(y≥0)千万元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
为了解甲、乙两厂产品的质量,从甲厂生产的产品中随机抽取3件样品,从乙厂生产的产品中随机抽取4件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图.若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
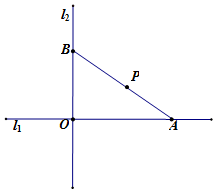 如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点.
如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com