Question

13．一个结晶体的形状为平行六面体ABCD-A₁B₁C₁D₁，以顶点A为端点的三条棱长都相等，且它们彼此的夹角都是60°，则$\frac{A{C}_{1}}{AB}$=（　　）

• A． $\sqrt{3}$
• B． 2
• C． $\sqrt{5}$
• D． $\sqrt{6}$

Answer 1

分析 根据已知条件可知该平行六面体的每个面都是菱形，所以可设边长为1，通过已知的角可判断向量$\overrightarrow{A{A}_{1}}与\overrightarrow{{A}_{1}{B}_{1}}，\overrightarrow{A{A}_{1}}与\overrightarrow{{B}_{1}{C}_{1}}$，以及$\overrightarrow{{A}_{1}{B}_{1}}与\overrightarrow{{B}_{1}{C}_{1}}$的夹角，从而可通过$|\overrightarrow{A{C}_{1}}|$=$|\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{B}_{1}}+\overrightarrow{{B}_{1}{C}_{1}}|$=$\sqrt{（\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{B}_{1}}+\overrightarrow{{B}_{1}{C}_{1}}）^{2}}$求出AC₁，从而可求得$\frac{A{C}_{1}}{AB}$．

解答 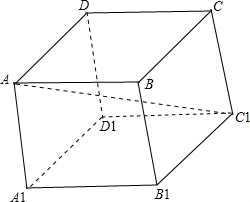解：如图，根据已知条件设该平行六面体的边长为1，则：
$|\overrightarrow{A{C}_{1}}|$=$|\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{B}_{1}}+\overrightarrow{{B}_{1}{C}_{1}}|$=$\sqrt{（\overrightarrow{A{A}_{1}}+\overrightarrow{{A}_{1}{B}_{1}}+\overrightarrow{{B}_{1}{C}_{1}}）^{2}}$=$\sqrt{1+1+1+2•\frac{1}{2}+2•\frac{1}{2}+2•\frac{1}{2}}=\sqrt{6}$；
∴$\frac{A{C}_{1}}{AB}=\sqrt{6}$．
故选D．

点评 考查了菱形的概念，用向量解决立体几何问题的方法，以及空间向量的加法，求空间向量长度的方法，以及空间向量的数量积的计算．