
分析 由$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{\frac{1}{2}×AB×AD×sin∠BAD}{\frac{1}{2}×AC×AD×sin∠CAD}$,sin∠BAD=sin∠CAD,得到$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{AB}{AC}$=2,由此能求出$\frac{sin∠B}{sin∠C}$的值.
解答 解:∵在△ABC中,D是BC上的点,AD平分∠BAC,△ABD的面积是△ADC面积的两倍,
∴$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{\frac{1}{2}×AB×AD×sin∠BAD}{\frac{1}{2}×AC×AD×sin∠CAD}$,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴sin∠BAD=sin∠CAD,
∴$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{AB}{AC}$=2,
∵$\frac{AB}{sin∠C}$=$\frac{AC}{sin∠B}$,
∴$\frac{sin∠B}{sin∠C}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查三角形中两角正弦值的求法,涉及到三角形面积公式、正弦定理等知识点,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想,是中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如右图所示,则该几何体的体积为( )
一个几何体的三视图如右图所示,则该几何体的体积为( )| A. | $\frac{5}{3}$ | B. | $\frac{{10\sqrt{3}}}{3}$ | C. | $\frac{10}{3}$ | D. | $\frac{{5\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,4) | C. | (1,4] | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
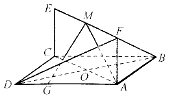 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB=$\sqrt{2}$,AF=1,G为线段AD上的任意一点.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB=$\sqrt{2}$,AF=1,G为线段AD上的任意一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com