练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若cos(α＋β)＝，cos(α－β)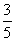＝，则tan αtan β＝________.


    解析　由已知，得cos αcos β－sin αsin β＝，cos αcos β＋sin αsin β＝，则有cos αcos β＝，sin αsin β＝，＝，即tan αtan β＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知角α的终边过点P(－8m，－6sin 30°)，且cos α＝－，则m的值为

    (　　)．　　　　　　　　　　　　　　　　　

    A．－           B.               C．－          D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝sin(2x＋φ)(－π＜φ＜0)，y＝f(x)图象的一条对称轴是直线x＝.

    (1)求φ；

    (2)求函数y＝f(x)的单调增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线y＝2与函数f(x)＝2sin2ωx＋2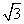sinωxcosωx－1(ω>0)的图象的两个相邻交点之间的距离为π.

    (1)求f(x)的解析式，并求出f(x)的单调递增区间；

    (2)将函数f(x)的图象向左平移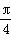个单位长度得到函数g(x)的图象，求函数g(x)的最大值及g(x)取得最大值时x的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知cos＋sin α＝，则sin的值是(　　)．

    A．－         B.            C．－           D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    ．在△ABC中，C＝60°，AB＝，BC＝，那么A等于(　　)．　　　　　　　　　　　　　　　　

    A．135°          B．105°         C．45°           D．75°

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，△ABC中，AB＝AC＝2，BC＝2，点D在BC边上，∠ADC＝45°，则AD的长度等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


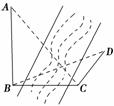
    如图，为测得河对岸塔AB的高，先在河岸上选一点C，使C在塔底B的正东方向上，测得点A的仰角为60°，再由点C沿北偏东15°方向走10米到位置D，测得∠BDC＝45°，则塔AB的高是________米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    △ABC的三个内角成等差数列，且＝0，则△ABC一定是(　　)．

    A．等腰直角三角形                      B．非等腰直角三角形

    C．等边三角形                          D．钝角三角形

    查看答案和解析>>

    同步练习册答案