
分析 (1)根据条件求出圆心和半径即可求出圆的标准方程.
(2)根据直线和圆的位置关系进行求解即可.
解答 解:(1)线段AB的中点为$(\frac{1}{2},\frac{3}{2})$,又kAB=-1
故线段AB的垂直平分线方程为$y-\frac{3}{2}=1•(x-\frac{1}{2})$即x-y+1=0…(2分)
由$\left\{\begin{array}{l}x-y+1=0\\ x+y+5=0\end{array}\right.$得圆心C(-3,-2)…(4分)
圆C的半径长$r=|AC|=\sqrt{{{(0+3)}^2}+{{(2+2)}^2}}=5$
故圆C的标准方程为(x+3)2+(y+2)2=25…(6分)
(2)令z=3x-4y,即3x-4y-z=0
当直线3x-4y-z=0与圆C相切于点P时,z取得最值…(8分)
则圆心C(-3,-2)到直线3x-4y-z=0的距离为$d=\frac{|-9+8-z|}{{\sqrt{{3^2}+{{(-4)}^2}}}}=5$,解得z=-26或z=24
故3x-4y的最小值为-26,最大值为24…(12分)
点评 本题主要考查圆的标准方程的求解,利用直线和圆的位置关系是解决本题的关键.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l⊥α,m⊥β,l⊥m⇒α⊥β | B. | l∥m,m⊆α⇒l∥α | ||
| C. | l⊆α,m⊆α,l∥β,m∥β⇒α∥β | D. | l⊥n,m⊥n⇒l∥m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
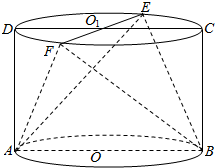 在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.
在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,|x|≥0 | B. | ?x∈R,|x|>0 | C. | ?x∈R,|x|≥0 | D. | ?x∈R,|x|<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>ab | B. | ab<b2 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | $\frac{b}{a}$>$\frac{a}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com