练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．如果a＞b＞0，那么下列不等式成立的是（　　）
    A．a2＞abB．ab＜b2C．$\frac{1}{a}$＞$\frac{1}{b}$D．$\frac{b}{a}$＞$\frac{a}{b}$

    分析 利用不等式的基本性质即可判断出结论．

    解答 解：∵a＞b＞0，
    ∴a2＞ab，ab＞b2，$\frac{1}{a}＜\frac{1}{b}$，b2＜a2即$\frac{b}{a}＜\frac{a}{b}$．
    故选：A．

    点评 本题考查了不等式的基本性质，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知圆心为C的圆经过点A（0，2）和B（1，1），且圆心C在直线l：x+y+5=0上．
    （1）求圆C的标准方程；
    （2）若P（x，y）是圆C上的动点，求3x-4y的最大值与最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设a＞b＞0，c≠0，则下列不等式恒成立的为（　　）
    A．$\frac{1}{a}$＞$\frac{1}{b}$B．ac＞bcC．$\sqrt{a}$＞$\sqrt{b}$D．$\frac{a}{c}$＞$\frac{b}{c}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．如图，已知F1（0，-1），F2（0，1）为椭圆Γ：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点，过F1作两条倾斜角互补的直线l1，l2，l1，l2分别与椭圆Γ相交于A，B，C，D四点，且△ABF2的周长为8．
    （Ⅰ）求椭圆Γ的方程；
    （Ⅱ）求阴影部分S的最大值；
    （Ⅲ）求证：直线AD与直线BC的交点是定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．“x≠1“是“x＜1”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既非充分也分必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．圆O1：x2+y2-6x-4y-3=0和圆O2：x2+y2-4y=0的位置关系是（　　）
    A．相离B．相交C．外切D．内切

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．某几何体的三视图如图所示，则该几何体的表面积为（　　）
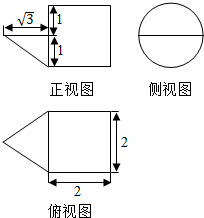
    A．$\frac{13π}{2}+\sqrt{3}$B．$\frac{（12+\sqrt{3}）π}{6}$C．$\frac{15π}{2}$D．$\frac{（6+\sqrt{3}）π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=loga（-x-1）+loga（x+3），其中a＞0且a≠1．
    （1）求函数f（x）的定义域；
    （2）求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设数列{an}的前n项和为Sn．已知a1=1，$\frac{{2{S_n}}}{n}={a_{n+1}}-\frac{1}{3}{n^2}-n-\frac{2}{3}$，n∈N*．
    （1）求a2的值；
    （2）求数列{an}的通项公式；
    （3）在数列{bn}中，${b_n}=\frac{4n+2}{{{a_n}•{a_{n+1}}}}$，求{bn}的前n项和Tn．

    查看答案和解析>>

    同步练习册答案